Here I am again with part 2. If you would like to read part 1 of this short tutorial on copulas, please click here.
In this second post I am going to select a copula model, fit it to a test dataset, evaluate the fitting and generate random observations from the fitted multivariate distribution. Furthermore I am going to show how to measure correlation using Spearman's Rho and Kendall's Tau. In order to run the code in this post you need the following packages: copula and VineCopula.
The dataset
For this example I am going to use a test dataset. You can download it from this link. This test dataset contains two variables, x and y, characterized by a strong left tail correlation.
By visually inspecting the plot of x versus y you can easily notice that low values of x tends to be highly correlated with low values of y.
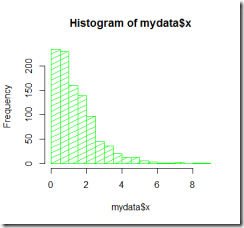
The x and y distributions
First of all, let's study the marginals separately. Coming up with an estimate of the marginal distributions for both x and y should not be that hard. In order to do this, a quick check to the histogram of both variables could provide some insights.
A good glimpse at the chart of each variable is important in order to get a grasp of what distribution could be a better fit. It looks like a Gamma distribution could do both for x and y. This is just a quick guess, obviously it would be necessary to dig deeper and inspect the data further before making such a claim, however this is not the focus of this post. Moving on pretty fast and assuming the distribution assumption is correct, the only thing left is to estimate the parameters. Let’s estimate the parameters, sample some observations from the fitted distributions and make a visual comparison.
You can see in green the observed data and in blue the simulated data for both x and y. That looks like a good match.
Measures of association Kendall tau, Spearman's rho
Now it's time to look at the joint behaviour. For instance, we could measure the association between x and y. When dealing with copulas, two common measures of association are Kendall's Tau and Spearman's Rho. These two are usually better suited for measuring association than linear correlation measures when working with copulas. I am going to use Kendall's Tau
Take note of the output of this code because later, when you will have fit the copula model, you will be able to check that the same correlation structure has been preserved (or captured, if you wish) by the copula.
Selecting the copula using VineCopula package
Since we are dealing with a bivariate case, we can use a scatterplot to get an idea of what the joynt relationship of x and y looks like and try to understand the joint behaviour of the two variables. As you know, the joint behaviour is captured by the copula, therefore by taking a look at it we can try to guess what copula might fit.
Of course a guess is not the optimal way of selecting a model, furthermore the "visual guessing method" is not applicable in case we have more than 3 variables, so we are going to use a useful function provided by the Vinecopula package.
The VineCopula package provides a convenient way of choosing a copula through the BiCopSelect() function. The VineCopula library performs copula selection using BIC and AIC.
Note that BiCopSelect() accepts pseudo observations as parameters. That is, the fitting process is performed on the pseudo observations, ie the observations in the unit square $[0,1]^2$. The pobs() function takes care of the conversion from real observations to pseudo observations. Note that pobs() returns a matrix (not a dataframe!).
It appears that a Clayton copula might be a good choice for our problem. The unique parameter of the Clayton, theta, is estimated to be 1.48.
Fitting process with a given copula
The BiCopSelect function, estimates the copula parameters too. However, in case you already know what copula to use, you could fit it using the fitCopula() function.
It looks like the fitting process was successful and the parameters of the fitted copula are the same estimated with the BiCopSelect() function. That's a good double check, by the way. Note that Kendall's tau is the same as the one calculated from the observed x and y.
Goodness of fit test
Once the copula has been fitted, we can test to check whether the fit is good or not. In order to perform this GOF test, we can use the gofCopula() function as below. Note that this test may be a little slow to run.
For comparison, I decided to run it twice, first with a normal copula and then with a Clayton.
Building the bivariate distribution using the copula
Now that we have successfully chosen and fitted the copula to the data and selected the appropriate marginals, we can try to model the joint relationship using the basic tools I showed in part 1 of this short tutorial.
Now we can sample some observations from the estimated joint distribution and check how they compare to the one observed.
Sample observations from the brand new bivariate distribution
Simply use the tools I explained in part 1 to sample from the new built distribution.
Note that Kendall's tau is still the same for the simulated data. The information about the correlation structure has been captured by the copula regardless of the marginals. Of course this is just a taste of how powerful plain vanilla copulas, such as Archimedean copulas, can be.
At the top of my mind I cannot think of other “easy to use” tools for modelling "weird" relationships such as the one between x and y in my test dataset.
I hope this two parts post was useful and interesting. Please feel free to leave a comment if you have any question or spot any mistake.








thank you! it was very helpful.
ReplyDeleteThanks for reading!
DeleteThis comment has been removed by the author.
DeleteHi, at the moment I'm working on two R-related projects, I'm afraid I do not really have any spare time. However, if you need to hire an R developer to build a model for you, I should be free after march 2017. Please use the contact form in the "contact" page. Rates will vary upon the project required. If that is not the case, or if you need just a quick help, I suggest you to ask questions on Crossvalidated at https://stats.stackexchange.com/ where there are expert and polite people ready to answer your questions in depth.
DeleteMic you have done nice work here, congrats!
ReplyDeleteI have a question regarding copulas,
When we search for a type of correlation between two variables and we have almost fitted a BiCopula like you, it is necessary to continue with building of distribution and after search for " cor(mydata, method = "kendall") " ? Or after fitting of copula it is right to search for correlation?
Hi, thanks for your comment! I guess it depends on what you'd like to do, the idea behind the correlation checks in the post is to show that the structure of the data is preserved through the copula.
DeleteThanks Mic, keep coding!
DeleteThank you very much.
ReplyDeleteI was looking for a beginner level data and example and I found that!!
Thanks again!
Thank you for reading!
DeleteHi Mic! Nice post! I still have a question though..I'm also currently working on a project where I have to calculate VaR of different market indices for different periods after fitting several copulas. However, copulas have proven to be quite a challenge for an average master student. My code returns the same VaR for all the periods..so clearly I'm missing/overlooking something..can you tell me where (in your explanation) I should apply VaR?
ReplyDeleteThanks!
Hi Maarten! Thanks!Indeed they are quite challenging! I'm a bit rusty when it comes to VaR, however, I believe that having the pdf, the cdf and being able to simulate observations should be enough to start. Having said this, you need to make some assumption about the distribution of the returns/indeces/phoenomena that you are trying to model, choose the copula, fit it, then get the multivariate distribution that in my code I called "my_dist". Once you're there, you can get the density using dMvdc, the cdf using pMvdc and simulate observations using rmvdc (for instance for a Monte Carlo VaR).
DeleteHi Mic! It was really useful for me. Thanks for that!
ReplyDeleteI've started working with R 2 weeks ago and I am consider if there is Mardia copula also in some package?
Thanks!
Ola
Hi Ola! Glad to know you found it useful! As far as I know the best copula packages in R should be "copula" and "VineCopula". Both packages feature Archimedean copulas. In the documentation, however, there seems to be no mention about Mardia's. Maybe you can ask the developers if they plan to add that particular copula.
DeleteHi Mic, thank you for your quick response. That's great that I have possibility to speak with you! Yes, you're right, I read documentation for "copula" and "VineCopula" many times and there is no mention about Mardia. I've tried to put formula for Mardia copula and then built bivariate distirbution with specified marginals in the fallowing way:
Delete> df<-read.table("R_popr.txt", header = TRUE)
> xy<-df[,c("x","y")]
> m<-pobs(xy$x)
> mm<-pobs(xy$y)
fun<-function(u,v) 0.1*u*v+0.4*max(0,u+v-1)+0.5*min(u,v)
mardia<-asCOP(m,mm,fun)
mycdf<-mvdc(mardia, margins = c("exp","exp"), paramMargins = list(list(rate=2),list(rate=2))))
but I got error:
Error in validObject(.Object) :
invalid class “mvdc” object: invalid object for slot "copula" in class "mvdc": got class "numeric", should be or extend class "parCopula"
As we see, the two datasets have a similar structure. This is evidence that the proposed model is appropriate.
Could you please advise on above?
Also, I tried to compare empirical copula with the theoretical one, but I encouner the problem. It is easy to use cdfcomp when argument ft is a list of "fitdist" objects - so for example in case of fitting copula without specified marginals, but it is no possible to compare distributions of object mvdc using cdfcomp. Do you know how the comparison of pdf's can be done for mvdc object? The same problem is with gofCopula.
Sorry that I have so many questions to you :)
Thank you,
Ola
Hi Ola, it seems that the problem is that in your example you're passing to the copula::mvdc function an object that is not of class "parCopula". The "mardia" argument is not a copula from the copula package but (probably) a numeric vector. More generally, since the "mardia" object seems to have been generated using the function copBasic::asCOP, I think that the packages copBasic and copula may not be compatible with each other. This means that if you build the Mardia copula with the copBasic package functions, it probably won't be accepted as an argument in most of the functions in the copula (and probably vinecopula too) package.
DeleteMy suggestion is to clearly define what your goal and steps are, then look for a suitable R package and stick to it. If you have specific questions on your project, you can try to ask on CrossValidated (https://stats.stackexchange.com/). People there are usually very competent in their subjects and nice, although I must say there's not that much on copulas there either.
As a last suggestion, if you are doing this for work or study, I suggest you to get in contact with some good university professor/PhD that might be willing to help with the project (Masters student in stats might be interested in writing a thesis on an R implementation of the mardia copula and related functions/tests/applications).
I wish you all the best.
Mic
Great two-piece article. I have a question though.
ReplyDeleteBased on a given copula and known marginals.. if I wanted to know what is the probability of y for a given x ? Or what is the ratio of the copula probabilty for given values of x and y compared to the independent case. The independent case would just be a multiplication of the respective marginal densities for x and y. Is there a command I could use in the Copula or VineCopula package?
Thanks for your help!
Hi, maybe this question on stackexchange can help you, it seems to address your question: https://stats.stackexchange.com/questions/90283/how-to-find-conditional-probability-pxxy-y-using-copulas
Deletehow to estimate the Value at risk of a portfolio composed of 2 assets using the copula approach and how to do the backtesting ? i need the R codes please
ReplyDeleteHi,
ReplyDeleteThanks for the useful post. I'm trying to follow this example using my own data. In my case BicoSelect gives a Tawn type 2 copula. However, I'm getting an error when fitCopula to this copula type" :
"Error in (function (classes, fdef, mtable) : unable to find an inherited method for function ‘fitCopula’ for signature ‘"function"’"
Any idea what's going on here?
Thanks!
I really appreciate for this wonderful lesson.I am working on my project. I am looking to generate data from the bi variate distribution which I develop. So Could you please help me in simulating data in R. Your post is helpful but it is only for known distribution.Anyway if you have time, you can email me. Thank you for your help
ReplyDeleteHi Mic, the post was very helpful and I am very grateful of your efforts.
ReplyDeleteI am new in working with package vine copula. But I have problem with package which is as follow.
My purpose is to combine 3 hydrological indices in VineCopula package in order to obtain a single index which encompasses the marginal distribution of the all 3 hydrological indices. The procedure that I did is as follow:
1. Finding the best distribution for each index and transfer the indices to [0 1] base on their optimal distribution.
2. Forming the best structure and copulas (which is 3 dimensional) using RVineStructureSelect in vine copula package.
3. Simulate the data sets using RVineSim in order to compare the simulated data with original data sets which turns out to have good agreement with original data sets.
In the final step I am confused how to obtain the final index (I have mentioned before) which should have the marginal properties of all 3 hydro… indices.
I will be grateful if you help me out with my problem.
Thanks!
Zahir
Hi Zahir,
DeleteI am working on an undergraduate project at IIT Kharagpur, India. As a novice in this topic, I am facing difficulties in implementing the case where I have multivariate marginal distribution function. My project sub-part is almost similar to yours.
Therefore, It will great help if you help me in clearing few of my doubts. Please contact me @ sauravk082@gmail.com.
Thanks and welcome.
Sauav
The Topic on the Copula distributions is beautifully presented..Thank you..:)
ReplyDeleteHi MIC, I am new in this field of copula and from your tutorial i reached upto fitcopula but in gofcopula it shows error as(Error in optim(start, logL, lower = lower, upper = upper, method = optim.method, :
ReplyDeletenon-finite value supplied by optim
In addition: Warning message:
In .gofPB(copula, x, N = N, method = method, estim.method = estim.method, :
argument 'ties' set to TRUE)
please help me to fix this issue
Hello Mic,
ReplyDeleteand thank you for your nice code and comments. Everything works fine, but the line:
sim <- rmvdc(my_dist, 1000)
which could be replaced by:
sim <- rMvdc(1000, my_dist)
In case you need help with any kind of relationship issue no matter how difficult they are or you want to cure any kind of diseases, need a good job or instant fast growing wealth in your business write to Prophet Ibuda right now via facebook page https://www.facebook.com/prophetibuda/ and phone number +2348100663964 email uniquelunarseer@ gmail com for help and assistance. You can have a glimpse of what he can do for via his website https://prophetibuda.wixsite.com/seer be it
ReplyDelete(1) If you need to get an ex back to your life,
(2) If you want a divorce spell to divorce your narcissist lover without any trouble,
(3) If you love your current lover but you want him or her to love you more and even care ore towards you.
(4) If need attraction and bond to the right person whom will love and treat you as you want.
Hi Mic
ReplyDeleteThanks for the codes you've provided in part 1 and part 2.
Please help and provide the R code for estimating BB1 copula parameters and the R code for the goodness of fit test for the BB1 copula.
I am new in using vine copulas and i will greatly appreciate your assistance.
Regards
HB
i am also unable to use the fitcoupla function
ReplyDeleteMy name is donald boykins , am here to appreciate Dr Akhigbe for using his herbal medicine to cure my Herpes virus. Is about 3 years and 6 months now I have been living with this virus and it has been a serious problem to me, I was so confused cause i have been taking several drugs to be cured but all of my effort was in vain,one morning I was browsing through the internet then I saw several testimonies about Dr. Akhigbe curing people from Herpes virus and immediately i contacted Dr. Akhigbe on his email: drrealakhigbe@gmail.com, i told him about my troubles and he told me that i must be cured, he gave me some instructions and which i rightly followed. so he prepared a herbal medicine and sent it to me which i used for 2 weeks and i was cured everything was like a dream to me and my Herpes virus was totally gone, dr .Akhigbe, God bless you and give you more power and ability for more cure.I don't know if there is any one out there suffering for herpes virus or any of these diseases..DIABETES, CANCER, HIV/AIDS, HERPES HEPATITiS A AND B. FEVER, EPILEPSY, MENINGITIS, DENGUE SCHIZOPHRENIA, PROSTATE, THYROID, BACTERIA, MALARIA, DICK AND BREAST ENLARGEMENT,MULTIPLE SCLEROSIS, TUBERCULOSIS, DIARRHEA, POLIO, ARTHMA, LUPUS, RABIS, JOINT PAIN, STOMACH PAIN,, HEART DISEASE, CHRONIC DISEASE,EPILEPSY, LUPUS, STROKE, SPINAL CORD INJURY, ECZEMA, KIDNEY DISEASE, ACME, BACK PAIN etc. why don't you contact dr.Akhigbe today and be free from your diseases because he is very good and honest Doctor and he is also called the godfather of herbal root contact him via email; drrealakhigbe@gmail.com or whatsApp him on +2348142454860
ReplyDeletewebsite https:drrealakhigbe.weebly.com
Thank you so much, it was very beneficial and usefull for me as a beginner.
ReplyDeleteHOW I GOT CURED FROM HERPES VIRUS I was diagnosed of HERPES virus and i have tried all I can to get cured but all to no avail,,until I saw a post in a health forum about a herbalist man who prepare herbal medications to cure all kind of diseases including HERPES virus,at first I doubted if it was real but decided to give it a try,when I contacted this herbalist via his email and he prepared a HERPES herbal cure and sent it to me via UPS delivery company service, when I received this herbal medicine, he gave me step by direction on how to apply it,after applying theUPS delivery company service, when I received this herbal medicine, he gave me step by direction on how to apply it,after applying the. way I was instructed,I was totally cured of this deadly disease called HERPES, all thanks to Dr oboh.Email obohesan@gmail.com this great herbal doctor via WhatsApp+2348089281017 HE CAN ALSO CURE SICKNESS LIKE{1}HIV/AIDS
ReplyDelete{2}DIABETES
{3}EPILEPSY
{4} BLOOD CANCER
{5} HPV
{6} ALS
{7} HEPATITIS
{8}LOVE SPELL
{9} SICKLE AND ANAEMIA..
or via whatsapp +2348089281017
The greatest Joy in my life today is that i have been cured of Herpes by a Doctor called Dr.Kudera, I was infected with HERPES Disease in 2020, i went to many hospitals for cure but there was no solution, so I was thinking how can I get a solution, so that my body can be okay. Until one faithful day as i was browsing on the internet I saw a testimony on how Dr.Kudera has helped people in curing Herpes and other diseases, quickly I copied his WhatsApp number so i contacted him for solution for my Herpes disease, So Dr.Kudera told me that his going to prepare his herbal medicine for my health which he sent to me, luckily after 2 week my Herpes was cured. Dr.Kudera is well recognize as one of the best herbalist doctor in Africa, you don't have to be sad anymore or share your tears anymore on this disease when the cure is available. The medicine has NO SIDE EFFECT,there's no special diet when taking the medicine. He also cure ALS, HIV AIDS, CANCER, HPV, DIABETES and lots more.
ReplyDeleteFor enquiries:
WhatsApp: +2348146552606
Hello everyone. Dr Ishiaku herbs is a good remedy for herpes Virus , I was a carrier of herpes virus and I saw a testimony on how Dr. Ishiaku cure Herpes Virus, I decided to contact him, I contacted him and he guided me. I asked him for solutions and he started the remedies for my health. After he finish he sent me the herbs which i took for 2 weeks before asking me to go for a check up and getting there i could not believe that i was confirm HSV 2 Negative after the test, Today i am so happy because I'm free from herpes disease with the help of Dr. Ishiaku . Thank God now everything is fine, I'm cured by Dr. Ishiaku herbal medicine, I'm very thankful to God for making it possible. you can reach him on his email, i strongly recommend him to any one out here looking for a cure to herpes or any other deadly disease...Contact Dr ishiaku via email: ishiakuherbalcure@yahoo.com or whats-app +2348180828544
ReplyDeleteI have been suffering from a deadly disease (Hsv) for the past 2 years now, I had spent a lot of money going from one places to another, from churches to churches, hospitals have been my home every day residence. Constant checks up have been my hobby not until this faithful day, I was searching through the internet, I saw a testimony on how Dr Ehimare helped someone in curing his (Hsv) herpes disease, quickly I copied his email which is drehimare3@gmail.com just to give him a test I spoke to him, he asked me to do some certain things which I did, he told me that he is going to provide the herbal cure to me, which he did, then he asked me to go for medical checkup after some days after using the herbal cure, behold I was free from the deadly disease, he only asked me to post the testimony through the whole world, faithfully am doing it now, please brothers and sisters, he is great, I owe him in return. if you are having a similar problem just email him on Drehimare3@gmail.com Or whatsapp him via +1 (267) 691-1087
ReplyDeleteBefore people said there is no cure for herpes virus but today many people have now believe that there is a cure,herpes virus can be cured through Africans roots and herbs, dr.ubarlo he is the one of the great herbal doctor in Africa and he has the cure on this virus last month he share his herbal medicine in some medical hospital and now he is well recognize as one of the best in Africa, you don’t have to be sad any more or share your tears any more on this virus when the cure have already be find by dr.ubarlo email him on drubarlohome@gmail.com or Whatsapp number +2348119508814
ReplyDeleteA Good product.....
ReplyDelete100% guaranteed.,
Healed from Hsv_____
Visit..((Robinsonbuckler11 @)) gmail com
ReplyDeleteThe tutorial effectively guides through fitting a copula model in R using the VineCopula package. It covers data preparation, estimating marginal distributions (e.g., gamma), measuring association with Kendall's Tau, selecting an appropriate copula using BiCopSelect(), and fitting the copula with fitCopula(). The process includes assessing goodness of fit with gofCopula(), constructing a multivariate distribution with mvdc(), and generating random observations. Visual comparisons and correlation checks confirm the copula's ability to capture the joint behavior of variables, demonstrating its utility beyond traditional correlation measures.
https://goodsresponse.com/21ways-to-respond-to-i-want-you/
Thank you for this insightful guide on fitting copula models in R! Your step-by-step approach from selecting copula models to evaluating fitting and generating random observations is both clear and practical. I especially appreciate how you've demonstrated the use of Spearman's Rho and Kendall's Tau for measuring correlation, which are crucial when working with copulas.
ReplyDeletehttps://goodsresponse.com/21ways-to-respond-to-a-heart-emoji/
Have you been suffering from any kind of diseases, and you want to be free from it. Then contact, Dr. Joseph Olorungbebe. On his WhatsApp: +2347026909147 Or email: drjosepholorungbebe@gmail.com
ReplyDeleteFirst of all this the MOST AMAZING material I found on for Copula on website! Thank you so much Mic for your great work!
ReplyDelete2nd, if I may have one question that confuses me here:
>>> in your bivariate case, v<-rMvdc(5000, my_dist) gives you 2 series of data set, dim(v)= (5000, 2). Then pdf_mvd<-dMvc(v, my_dist) , this pdf_mvd is just an array of 5000 numeric numbers. So is this pdf_mvd a joint probability density? Thank you so much for your advice!
My name is Mrs Aisha Mohamed, am a Citizen Of Qatar.Have you been looking for a loan?Do you need an urgent personal loan or business loan?contact Adam Ibrahim Finance Home he help me with a loan of $80,000 some days ago after been scammed of $6,800 from a woman claiming to been a loan lender but i thank God today that i got my loan worth $80,000.Feel free to contact the company for a genuine financial service. Email:adamibrahimfinanceltd1976@gmail.com call/whats-App Contact Number +918119841594 Adam Ibrahim Finance Pvt Ltd
ReplyDelete