More than a year ago I wrote a short post on how to fit a copula model in R. The post showed how to make a very raw and basic fitting of a test dataset to a two dimensional normal copula (or a gaussian copula if you wish) using the copula package. The content of the post was not much, but that was a big part of what I knew about how to use copulas in R at that time and there was not much documentation available other than the official copula package documentation which is quite technical in my opinion (as it should be) and may not be that easy for a beginner copula user.
The main two reasons as for why I wanted to write a revised post are the following:
- I wanted to provide a better introduction to copulas in R than the one I wrote back then.
- By looking at my blog analytics I found out that a significant chunk of the people that visit my blog are looking for how to fit a copula model (or at least how to get started with it I guess) and I feel now I can offer better information to anyone interested in starting to use copulas.
This post is splitted in two parts:
- Part 1: This part introduces the beginner to the basic tools and functions you may need to work with copulas in R.
- Part 2: The second part addresses the selection of the copula, the fitting process, the evaluation of the fitting, some considerations and a practical example.
Since this post aims to be an introduction to copulas in R I assume you are somewhat familiar with at least elliptical and Archimedean copulas. In case you are not, but would like to be, I highly suggest this book on the topic. In my opinion it is one of the best resources for beginners: very well written and explained.
A quick reminder (just to put in some fancy equations)
Elliptical copulas
If you denote by $F$ the multivariate cumulative distribution of an elliptical distribution, $F_i$ the ith marginal and $F^{-1}$ its inverse, then you can build the following elliptical copula
$$ C(u_1, ... , u_n) = F (F_1^{-1}(u_1) + ... + F_1^{-1}(u_n)) $$
Archimedean copulas
An Archimedean copula can be obtained using a function $\phi$ called generator function as such
$$ C(u_1, ... , u_n) = \phi ^{-1} (\phi(u_1) + ... + \phi(u_n)) $$
For instance, the Gumbel copula is obtained using the following generator function:
$$-( \ln x )^{\theta}$$
and its inverse
$$ \exp( - y^{\frac{1}{\theta}} ) $$
The most common Archimedean copulas families are Frank, Gumbel and Clayton. These three are the copulas I am going to use further down this post.
Loading the required libraries
Let's load the packages you are going to need, set the random seed for reproducibilty purposes and dive in
Warming up with elliptical and Archimedean copulas. Generating the copula with known parameters
As you probably know, elliptical and Archimedean copulas have nice mathematical proprieties, shape and formulas. They are a good choice for the initial warm up. Assuming you already know the parameters, this is how you would generate a bivariate normal and a t copula
As you can see, the arguments are pretty much self-explanatory. The normal copula takes in two parameters: the dimension of the copula (2 in this case) and the $\rho$ parameter which can be estimated from the data as I am going to show in part 2 of this post.
The t copula accept another argument df which basically determines the shape of the copula and can be estimated from the data as for $\rho$. The copula package provides specific functions to generate each implemented copula model: the general form "name" + "Copula()" can be used to build Archimedean copulas as well. Archimedean copulas take only a single parameter $\theta$.
Generating the copula with specified marginals using mvdc
Again, as you probably already know, the main appeal of copulas is that you can essentially separate the marginals (marginal distributions) from the dependence structure and model them separately. This fact leads to a great simplyfication when trying to model the joint behaviour complex phenomena, mainly because the marginals are easier to model than the joint distribution. Furthermore, if you had to model the joint behaviour of, say more than 20 objects (for instance the life of 20+ capacitors in an electrical component), then you would probably have a hard time by going straight into modelling the joint behaviour while the marginal distributions may be easier to estimate.
The copula package provides a nice set of functions (mvdc, dMvdc, pMvdc and rMvdc) for modelling multivariate distributions using a copula.
Generating random samples from the copula
Once the copula has been fitted, you can easily generate random numbers by using rCopula method for the single copula or rMvdc for the multivariate distribution as below
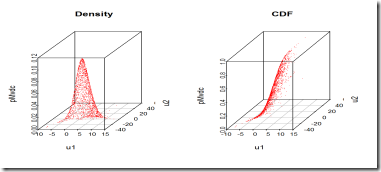
PDF and CDF
Computing the PDF and CDF of your copula may be useful for later use. Sticking to the R style, the copula package provides a density and a CDF function that are named using the same convention adopted in R: pCopula calculates the cumulative distribution (p stands for CDF) while dCopula calculates the density (d stands for PDF). Note that rCopula used for sampling observations follows the same basic R naming convention to. The same applies to pMvdc, dMvdc and rMvdc for multivariate distributions.
Now you only need some plotting functions in order to display the density and CDF properly.
Graphics
When making a presentation or presenting a model, graphics and images are essential. However, when high dimensionality is involved, the task of plotting some results in a visual way is quite challenging. The use of copulas is often related to high dimensional dependence modelling. But assuming that you are using bivariate copulas, you can plot the estimated density and the cumulative distribution function using the different approaches. For example you could plot a scatterplot of the density or a contour plot.
The copula package implements some useful methods for plotting contour plots that can be very helpful and sometimes are a good alternative to the more traditional 3d plots. Furthermore, when using a mvdc object and a copula with custom marginals the contour plot might be quite revealing about the density shape.
Below is the output of the script
Perhaps more interesting is the plot of the density and cdf of the multivariate distribution. Note how the scatterplot and the density plot can be misleading though. This is one of the reasons why in most cases I personally prefer to look at contour plots if they are available
A visual comparison of the density and CDF of the most common Archimedean copulas
It could be interesting to look at a visual take of the density of the Frank, Gumbel and Clayton copula. By using the methods available in the copula package you can easily do it. Note that I have chosen arbitrary parameters for the copulas.
stay tuned for part 2 of this post.







Dear Mic, have you done any trivariate copula analysis?
ReplyDeleteThank you.
KD
Hi KD, not yet on here. By using mvdc you can extend the example to a 3d copula though.
DeleteNo problem creating a 3D coupla, but how would you get slices to be able to visualize them using contour or curve?
DeleteThanks
Thanks for reading!
ReplyDeleteHello Mic, thanks for the great post, it inspire me to use copula for my research.
ReplyDeletecould i ask you question regarding how to use Ali-Mikhail-Haq Copula in this R syntax? I'm searching but couldn't found a clue about it.
Thank you for your time Mic.
Moshi
Hi Moshi! Thanks for your comment! I'm glad to know that!
DeleteSure, ask me!
hello Mic, instead the AMH Copula (since my prof reject it because lack of source in my native language), i wanna ask your help regarding the 3d plot and contour plot
Deletehow to intepret the result of the 3d PDF and CDF plot and contour plot of the copula? i'm confused with the negative x graph and y graph. thanks before x)
Hi Moshi2Arf, thanks for passing by! A copula is always contained in the 0-1 range (in the case of 2 dimensions, a bivariate copula is an application from I^2 to I where I = [0,1]), however, when you use a copula to generate a multivariate distribution, that new multivariate distribution isn't usually in that domain (unless you have normalized your data in the 0-1 interval). Its range will depend on the scale and on the empirical distribution of the data you used to obtain that model.
DeleteI think that the 3d PDF and CDF graphs you are referring to are not copulas. Looking back on my post I may have not made that very clear when I presented the results.
Remember that the copula is used to describe the dependence structure only. However, you are usually interested in obtaining a distribution for the phoenomena you are trying to understand. That phoenomena is (usually) not in the 0-1 range.
hi,
ReplyDeletecan we use Copula for predicting the value just similar to Linear multi-variant regression model. Dividing input data set into training data and testing data to predict the outcome.
kindly reply
I can't load 'copula package', kindly help me. When I'm trying to load 'copula' package from Packages drop-down menu in R, it gives me the following error:
ReplyDeleteError: package or namespace load failed for ‘copula’ in loadNamespace(j <- i[[1L]], c(lib.loc, .libPaths()), versionCheck = vI[[j]]):
there is no package called ‘gsl’
I'm now able to load the 'copula' package.
ReplyDeleteHi Mic, it is a really usefull post. Could you teach us to do trivariate copula with mlp and AIC and KS test for it.
ReplyDeleteThank you
Hi Mic, it helps me a lot, but I was wondering how to combine Copula with Bayesian networks. Do you have any enperience in that? Thanks a lot!
ReplyDeleteReally helpful, informative post! Thank you and keep up the good work!
ReplyDeletekindly send me the commands how to get AD and IAD statistic value for goodness of fit for copula function.
ReplyDeleteExcusme sir, do you know how to estimate Y value from bivariat Copula (X & Y in training split) dependency if we know the X value?
ReplyDeleteDear Mic, I need help for fitting and Plots of Newly Defined Bivariate distributions. Thanks.
ReplyDelete