Today while I was applying some of my knowledge of Financial Mathematics, I came across a weird problem. Ok I guess that’s not that weird after all, however I did not find at first, a formula or some trick to get to my goal and therefore I decided to use a simple approximating algorithm.
Say you have some data on a fixed-rate mortgage, a really basic mortgage where both the interest rate and the annual payment are fixed. By the way, if you’d like to know more on these mortgage check the wikipedia page here.
Apparently, the expression used to determine the annual payment, given the initial conditions, should be the following:
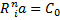
![clip_image002[6] clip_image002[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhVQUzVTkHfpIwpkCdmy2oaJUL3eeOFXF1D9IzoPqETME3Pu1sP-j94lrh1Nz3UvVp4PjDQkdWdth75pUs57iBYH67ECjqm0IC8b36lJtreEoc-SGYcML1UhnUbiehZWTw81-vnLRnu8O0/?imgmax=800)
![clip_image002[12] clip_image002[12]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiyRvLarFpKTsSGSte7-_WF3rR7Dkl__DXBFtPIQy7EbwJF-Ip4zkfQQ_Byy2BYieN4bq_vVMrV-UfDuf5GBrKKcf6jcd-TTssh1y3NOR3IJRyzYICfYbwzTLhxpuXksyQY6jGduWFg4yM/?imgmax=800)
Now, suppose that you have everything, the annual constant payment (R), the initial capital (C0), the number of years (n) and you want to find the interest rate applied (i).
At first, it may appear difficult to deal with this problem analytically, so my first idea to get around this was the following: first, define k as the ratio of the initial capital to the annual payment C0/R, then rearrange the equation in terms of k as follows
![clip_image002[14] clip_image002[14]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjqb5L1GjzcmaJ5RTXBKoGx-8iCoRtNdyCj2Mzyb9Zny9gdbce9R5kdPYftIzqYw99HTEKH8V5U82XVTiLvf7mXHeZQcozvcyC9bCFJoFg6OuZ6kw91dytTQIU6NmkmaKH43U0GFeRQFPY/?imgmax=800)
Now the problem sums up to this: find the i that satisfies the following system of equations
![clip_image002[16] clip_image002[16]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi7PVGVu3j_MzNDXhqtKynYBjamNchpgNT90XCXyPubNaioZbvekN4abtTEdpEAynH6Y06AgDpRURAG12ojRk-uAecYxmMSfF9Blo7Q2qfrgATbBj6azfMDbYsL3NiZDWCMGJO9WpuL9bw/?imgmax=800)
Eventually, here is an algorithm in python to solve the system above
And here is the final plot

Hope this was interesting. Here is Wolfram Alpha’s answer for your reference. For some reason it outputs 0.079 while I get 0.0724 which was the random rate I used to build this simple example. Perhaps some mistake occurred. If you find out please let me know.
Disclaimer
This article is for educational purpose only. The numbers are invented. The article may well contain mistakes and errors. You should never use this article for purposes different from the educational one. The author is not responsible for any consequence or loss due to inappropriate use.

![clip_image002[16] clip_image002[16]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi7PVGVu3j_MzNDXhqtKynYBjamNchpgNT90XCXyPubNaioZbvekN4abtTEdpEAynH6Y06AgDpRURAG12ojRk-uAecYxmMSfF9Blo7Q2qfrgATbBj6azfMDbYsL3NiZDWCMGJO9WpuL9bw/?imgmax=800)
