Biot-Savart law: magnetic field of a straight wire

Magnetism and magnetism related phenomena are fascinating almost for everyone, in fact, I remember being a intrigued by the interaction between magnets since I was a little kid. On the other side, Python is great for plotting vector fields, although now that I am using also Matlab I found out most functions in numpy and matlab are similar to those used in Matlab (I don’t know who got inspired by who though).

Here is a small sketch of a vector field. Remember the Biot-Savart law for a straight infinitely long wire, which (assuming the current is flowing upwards) looks something like this:

Below is a 3d representation of the vector field and the Python code used to generate it. The tricky part (if I’m allowed to say so) is that you need to convert the value of the vector field from cylindrical coordinates into cartesian coordinates in order to plot it. Perhaps there’s a way to plot a vector field using also spherical and cylindrical coordinates however I still do not know how to do that.

	from mpl_toolkits.mplot3d import axes3d
	import matplotlib.pyplot as plt
	import numpy as np
	x = np.linspace(-4,4,10)
	y = np.linspace(-4,4,10)
	z = np.linspace(-4,4,10)
	x,y,z = np.meshgrid(x,y,z)
	# 3d figure
	fig = plt.figure()
	ax = fig.gca(projection='3d')
	def B(x,y):
	i = 1 #Amps in the wire
	mu = 1.26 * 10**(-6) #Magnetic constant
	mag = (mu/(2*np.pi))*(i/np.sqrt((x)**2+(y)**2)) #Magnitude of the vector B
	by = mag * (np.cos(np.arctan2(y,x))) #By
	bx = mag * (-np.sin(np.arctan2(y,x))) #Bx
	bz = z*0 #Bz (zero, using the right-hand rule)
	return bx,by,bz
	def cylinder(r):
	phi = np.linspace(-2*np.pi,2*np.pi,100)
	x = r*np.cos(phi)
	y = r*np.sin(phi)
	return x,y
	# Plot of the fields
	bx,by,bz = B(x,y) #Magnetic field
	cx,cy = cylinder(0.2) #Wire
	# Plot of the 3d vector field
	ax.quiver(x,y,z,bx,by,bz,color='b',length=1,normalize=True)
	#Plot the magnetic field
	for i in np.linspace(-4,4,800): #Plot the wire
	ax.plot(cx,cy,i,label='Cylinder',color='r')
	plt.title('Magnetic field of a straight wire')
	plt.xlabel('x')
	plt.ylabel('y')
	plt.show()

view raw magnetic_field.py hosted with ❤ by GitHub

Hope this was interesting! :)

Spectrogram representation of the B note from a guitar

A spectrogram is a visual representation of the spectrum of frequencies as they change with respect of another variable (in our case time). Matlab offers a great function to plot the frequencies against time, therefore I decided to try it on the recordings I used in the previous post. Here is the result I got

	% Loading wav file
	[ip, fs] = wavread('B.wav');
	% Spectogram
	specgram(ip)

view raw spectrogram.m hosted with ❤ by GitHub

Now, some comments. This representation of the frequencies tells us that the stronger components of our signal are below 1.5 KHz (1500 Hz) which is what we expected, however it looks like there are no other significant frequencies above 7 KHz and this is weird since in our FT of the signal we found higher frequencies (although with lower magnitude). Notice how the the higher the magnitude in the FT, the longer the frequency appear in the spectrogram.

Now, by using a simple tool I generated another spectrogram which seems to contain also the higher frequencies the one in Matlab did not have.

This spectrogram is better in tune with our FT of the signal, since it shows that our signal has frequencies up to 15 KHz as the FT showed

The program I used to generate the second spectrogram is Spek, it is free, and fast, however it has very few options. Below are some useful links

http://spek.cc/

http://en.wikipedia.org/wiki/Spectrogram

Applying Fourier to a real signal: guitar musical note B

I recorded a sound from the second string of my electric guitar (musical note B) and made a .wave file out of it. By using Matlab I tried to separate the sound of the note from the background noise and made some experiments.

At first I wanted to use Python for doing this, since I’m more knowledgeable about that than Matlab, however it looks like the most common ways to open a .wave file (scipy.audiolab and similar) are not available for Python 3 yet (either that or I could not find anything). Matlab provides simple functions for handling .wave files and great graphing tools but I could not find something to convert bins into frequencies as the function in numpy does, therefore I’m not sure the frequencies in the graph are correct.

Anyway, you can download the recording at this link, and here is the time domain signal representation:

By taking the FFT of the signal and filtering out the frequencies we don’t need, we filter out the noise and/or sounds we don’t need. My filtering rule lets through all the frequencies above 200 and below 1600 Hz. Of course this is a very naive way of filtering, however that’s a start.

You can play around and block out one, two, three peaks a time and hear the difference between the original recording and the edited one. Now, ideally B of the guitar should have a frequency of about 249 Hz (more or less), however it looks like the frequencies between 650 and 1020 Hz in our frequency domain representation are the main components of the note. Perhaps that’s because I messed up the bins. Anyway I’m glad that by applying a so simple filtering rule I’ve been able to remove the pitch sound at the beginning and smoothing out the musical note. Finally I also found out that Matlab has great publishing tools that enable you to print out an HTML file of your code, the results and graphs all together. Here is the code I used:

	% Loading wav file
	[ip fs] = wavread('B.wav');
	% B tone
	B = ip;
	% Play the recording
	sound(B,fs);
	% Plot the recording
	plot(B);
	ylabel('Amplitude');
	xlabel('samples');
	% Take the FFT of the recording
	n = length(B);
	track = B(1:n-1);
	FFT = fft(track);
	ft_mod = abs(FFT);
	bins = length(B)-1;
	% Find the fundamental frequency
	[max_value, max_location] = max(ft_mod);
	fundamental_frequency = (max_location-1)*fs/n;
	display(fundamental_frequency)
	display(max_location)
	% Frequency vector
	w = zeros(1,length(bins));
	for k = 1:1:bins
	w(k) = (k-1)*fs/n;
	end
	% Plot (half of) the FFT
	if mod(length(w),2) == 0
	index = length(w)/2;
	else
	index = (length(w)-1)/2;
	end
	plot(w(1:index),ft_mod(1:index)); hold on;
	xlabel('Frequency Hz');
	ylabel('Magnitude');
	title('FTT of the recording');
	% Apply a filtering rule (in this case I'm letting through only
	% frequencies between 200 and 1800)
	minFreq = 200; %400;
	maxFreq = 1600 ; %1100;
	for k= 1:1:length(w)
	if w(k) < minFreq || w(k) > maxFreq
	FFT(k) = 0;
	ft_mod(k) = 0;
	end
	end
	% Plot the edited FFT over the full one
	plot(w(1:index),ft_mod(1:index)); hold off;
	% Get back the recording
	y = ifft(FFT);
	% Play the result
	sound(abs(y),fs);

view raw fourier_B_note.m hosted with ❤ by GitHub

Calculate Fourier transform of a gaussian using Matlab

While wondering around in the Matlab documentation I found out there is a simple way to calculate the Fourier transform of any function using Matlab. Furthermore by using the function pretty() you can print out the result in a more friendly manner.

Let’s calculate for example the Fourier transform of the function u(x) = e^(-x^2). This calculation could also be done on paper: by applying the definition I wrote in the earlier article one finds out that:

Now, by using some properties of the transform (you can check them at http://en.wikipedia.org/wiki/Fourier_transform), we can play around and plot some functions. Here is the original function and its FT:

Let’s take the FT of e^(-(3x)^2)

It’s worth noting that when the function gets thinner, its FT gets more spread and viceversa. This phenomena is useful to understand the uncertainty principle.

This you tube video explains the link between this mathematical tools and physics.
https://www.youtube.com/watch?v=V7UNvDN_EZo

If you’d like to know more about the FT, check the wikipedia page:
http://en.wikipedia.org/wiki/Fourier_transform

Here is the Matlab code I used

	% Fourier transform calculation
	%-------------------------------------------------------
	% Declare symbols to use
	syms x t;
	% Parameters of the transform
	a = 300; %scaling
	b = 0; %shifting
	c = 0; %smoothing
	% Function to transform
	u = exp(-(a*t-b)^2) * exp(1i*c*t);
	% Transform of u
	uHat = fourier(u,t,x);
	% Printing u and u hat
	simplify(uHat);
	pretty(u)
	pretty(uHat)
	% Plotting
	x_axis = linspace(-15,15,500);
	figure;
	plot(x_axis,abs(subs(uHat,x_axis)),x_axis,abs(subs(u,x_axis)));
	xlabel('x');ylabel('y');
	title('Function and its Fourier Transform');
	legend('Fourier transform','function');

view raw fourier_transform.m hosted with ❤ by GitHub

Filtering an ideal signal with FFT

Hi everyone! Remember that in the last article I wrote that you can use the FFT to clean a signal from background noise? Well here is an example of signal filtering.

We start by generating a signal and then add some random noise using the random number generator in numpy. Here is the noisy signal:

Now, our signal is made up of two main frequencies: 20 and 30 Hz while the rest is mainly background noise. You can check this in the FFT of the signal:

Suppose we’d like to isolate the 20 Hz bit, that means we’d have to set to 0 each value in the Spectrum which is greater or lower than 20 Hz. Let’s block out everything outside 18 and 22 Hz and then apply the inverse FTT. Here is the signal we found (blue) compared to the exact signal we wanted to find (red). At the bottom of the graph there is the error between the two signals, notice that it is not that high, (at worst we missed 0.08, however on average we missed less).

Here is the python code I used to make this.

	import matplotlib.pyplot as plt
	import numpy as np
	import scipy as sc
	plt.style.use('ggplot')
	np.random.seed(20)
	#-------------------------------------------------------------------------------
	# Set up
	# Time
	t = np.linspace(0,1,1000)
	# Frequencies in the signal
	f1 = 20
	f2 = 30
	# Some random noise to add to the signal
	noise = np.random.random_sample(len(t))
	# Complete signal
	y = 2*np.sin(2*np.pi*f1*t+0.2) + 3*np.cos(2*np.pi*f2*t+0.3) + noise*5
	# The part of the signal we want to isolate
	y1 = 2*np.sin(2*np.pi*f1*t+0.2)
	# FFT of the signal
	F = sc.fft(y)
	# Other specs
	N = len(t) # number of samples
	dt = 0.001 # inter-sample time difference
	w = np.fft.fftfreq(N, dt) # list of frequencies for the FFT
	pFrequency = np.where(w>=0)[0] # we only positive frequencies
	magnitudeF = abs(F[:len(pFrequency)]) # magnitude of F for the positive frequencies
	#-------------------------------------------------------------------------------
	# Some functions we will need
	# Plots the FFT
	def pltfft():
	plt.plot(pFrequency,magnitudeF)
	plt.xlabel('Hz')
	plt.ylabel('Magnitude')
	plt.title('FFT of the full signal')
	plt.grid(True)
	plt.show()
	# Plots the full signal
	def pltCompleteSignal():
	plt.plot(t,y,'b')
	plt.xlabel('Time (s)')
	plt.ylabel('Amplitude')
	plt.title('Full signal')
	plt.grid(True)
	plt.show()
	# Filter function:
	# blocks higher frequency than fmax, lower than fmin and returns the cleaned FT
	def blockHigherFreq(FT,fmin,fmax,plot=False):
	for i in range(len(F)):
	if (i>= fmax) or (i<=fmin):
	FT[i] = 0
	if plot:
	plt.plot(pFrequency,abs(FT[:len(pFrequency)]))
	plt.xlabel('Hz')
	plt.ylabel('Magnitude')
	plt.title('Cleaned FFT')
	plt.grid(True)
	plt.show()
	return FT
	# Normalising function (gets the signal in a scale from 0 to 1)
	def normalise(signal):
	M = max(signal)
	normalised = signal/M
	return normalised
	#-------------------------------------------------------------------------------
	# Processing
	# Cleaning the FT by selecting only frequencies between 18 and 22
	newFT = blockHigherFreq(F,18,22)
	# Getting back the cleaned signal
	cleanedSignal = sc.ifft(F)
	# Error
	error = normalise(y1) - normalise(cleanedSignal)
	#-------------------------------------------------------------------------------
	# Plot the findings
	pltCompleteSignal() #Plot the full signal
	pltfft() #Plot fft
	plt.figure()
	plt.subplot(3,1,1) #Subplot 1
	plt.title('Original signal')
	plt.plot(t,y,'g')
	plt.subplot(3,1,2) #Subplot 2
	plt.plot(t,normalise(cleanedSignal),label='Cleaned signal',color='b')
	plt.plot(t,normalise(y1),label='Signal to find',ls='-',color='r')
	plt.title('Cleaned signal and signal to find')
	plt.legend()
	plt.subplot(3,1,3) #Subplot 3
	plt.plot(t,error,color='r',label='error')
	plt.show()

view raw fft_py.py hosted with ❤ by GitHub

Have fun!

Fourier Transform: first trials

The Fourier transform is surely one of the most amazing pieces of maths applied to the sciences. For starters it is defined as follows:

The definition is fine provided that you can take the integral of u(x) over R. (Technically you should say that u(x) belongs to L1(R). But aside from these technicalities, how awesome is that definition? Calculating the FT of a function with pen and paper isn’t that straight forward at all, except in some cases. It involves mainly using complex analysis techniques. If you are familiar with calculating “standard integrals” it is rare that you can apply the same techniques here.

But how can we apply this to something? Well it turns out that if you have a signal u(x) in the time domain, its Fourier transform is the signal representation in the frequency domain. Essentially the FT enables you to decompose your time domain signal into all the frequencies that make up that signal. A first simple application is deleting noise from a signal. By checking the signal spectrum (its FT) you can choose which frequencies you need to delete from the signal in order to remove the noise. Then you just apply the inverse FT and get back your time domain signal cleaned up (more or less). Now obviously the math behind this is hairy, however this should not scare you at all, and if you are interested in these subjects I suggest you to check out some resources to get a better grasp of how all of this works.

In order to compute the FT of a signal with Python we need to use the ftt function built in into Scipy. FTT stands for Fast Fourier Transform and it is a brilliant algorithm to speed up the otherwise very long calculation of the FT of a real signal.

The signal I’ve made is a linear combination of the sine and cosine function, pretty straightforward here is its representation in the time domain:

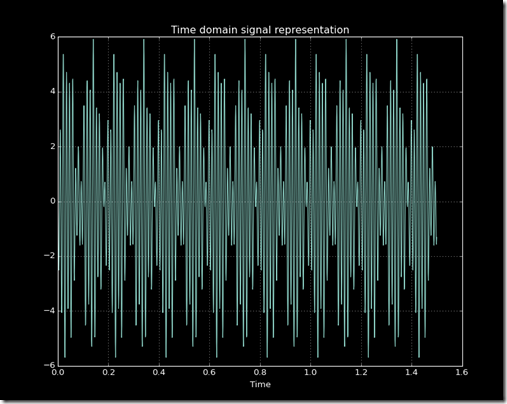
A closer look to our signal:

Now by taking the FFT we get a list of complex numbers. Then we take the absolute value of those numbers and plot them to represent the spectrum:

Eventually, we just need to fix the lower axis and switch from bins to Hz. Since the plot is symmetrical we can take out the right half without losing information. As you can see below, we have three spikes in the frequency domain. Those three peaks corresponds to the three frequencies we set earlier in the signal (85,50,75 Hz).

 

Hope you enjoyed this, soon I’ll make a post about applying this to a real signal, such as the recording of guitar notes. Below is the code I used to plot the data above. Have fun!

	import matplotlib.pyplot as plt
	import numpy as np
	import scipy as sc
	plt.style.use("dark_background")
	fs = 1000
	# Time
	t = np.linspace(0,1.5-1/fs,1500)
	# Frequencies in the signal
	f1 = 85
	f2 = 50
	f3 = 75
	# Signal
	x = 5*np.sin(2*np.pi*f1*t-0.5) + 2*np.cos(2*np.pi*f2*t-0.75) + 2.5*np.cos(2*np.pi*f3*t+1.2)
	# Take the FFT of the signal
	X = sc.fft(x)
	# The time domain representation of the signal
	# (use 350 to get the picture I got)
	def timeDomain(n=len(t)):
	plt.plot(t[:n],x[:n])
	plt.title("Time domain signal representation")
	plt.xlabel("Time")
	plt.grid(True)
	plt.show()
	# Plot the magnitude of the signal
	def magnitude():
	plt.plot(abs(X))
	plt.xlabel("Bins")
	plt.ylabel("Magnitude")
	plt.grid(True)
	plt.show()
	# Plot the frequency domain signal representation
	def frequencyDomain():
	freq = np.linspace(0,500,751)
	plt.plot(freq,abs(X)[:751],'r')
	plt.xlabel("Frequency Hz")
	plt.ylabel("Magnitude")
	plt.title("Frequency domain signal representation")
	plt.grid(True)
	plt.show()

view raw fourier_transform.py hosted with ❤ by GitHub