RC and RL are one of the most basics examples of electric circuits and yet they are very rich in content. Let’s examine each one carefully
Here is the schematics of an RL circuit
The components used in an RL circuit are a DC voltage source (V1) a resistor (R1) and an inductor (L1). The inductor in the schematics is used to represent physical characteristic of the circuit. If I had to describe what the inductor represents I would say it represents the ‘electrical inertia’ of the circuit. As currents flows into the circuit it generates a magnetic field, that change in the magnetic field causes a change in the flux of the field concatenated to the circuit, this in turn, by the Faraday-Neumann-Lenz law generates a voltage in the circuit that is opposite to the voltage that is generating the magnetic field (V1). This is the reason because the current in the circuit will not jump immediately to its full value of V/R given by Ohm’s law. The current will eventually reach the value V/R after an infinite amount of time, but for practical purposes we can consider it at that level after some time has passed (namely 4 times tau = L/R should be sufficient).
It so happens that, given the materials and the geometry, the inductance coefficients of the circuit I am modelling is 0.0229 H. Note that inductance depends only on these two parameters (materials and geometry). I calculated the coefficient using FEMM since the analytical calculation was not that easy to do. You can download FEMM here: http://www.femm.info/wiki/HomePage . This software is useful for many electromagnetic simulations and fairly user-friendly.
What we would expect is that the current will obey the following differential equation given by Ohm’s law at each point in time:
The equation above yields the following solution
Now, the same phenomenon (reversed) happens when you open the circuit, the inductor opposes the change in flux by generating a voltage that tries to keep up the shrinking flux of the magnetic field through the circuit. That means that, if you were to switch on and off the current at particular intervals you would obtain this behaviour:
As you can see, at time 0 the circuit is closed and the current is reaching its theoretical value, after 4 times tau (time constant of the circuit) the circuit is opened again and the current exponentially decays to zero. By knowing tau, one could find the frequency at which the switch should click in order to maintain this behaviour. This process yields the on and off cycle (in green). Where the green function hits the x axis the switch clicks and opens/closes the circuit.
Here below you can find the script I used to produce this graph and model the circuit.
If you are not satisfied with this crude simulation, perhaps you could use LTspiceIV which is a great free simulation software for electrical and electronic circuits. I used it to produce the schematics above and to simulate the behaviour of the current in the first 40ms after startup. Below is the LTspice simulation graph
As you can see by plotting the current through the resistor in LTspice, it seems our calculation were right!
Now let’s move on to the RC circuit, here it is:
Aside from the voltage source, the RC circuit is composed of a capacitor and a resistor, we therefore assume that self-inductance is negligible. When we close the circuit, there is no inductance here so the current will just jump to the V/R value and since the capacitor is charging up and building a voltage, we can expect the current at the resistor to drop as times goes by. The differential equation we have now is the following:
By solving it, one finds:
Therefore
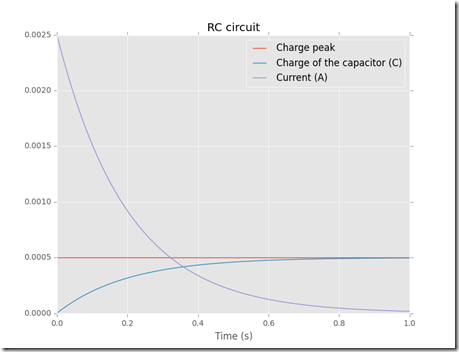
The current through the resistor drops exponentially, depending on a time constant tau = 1/RC. This behaviour is indeed what we find by running the simulation in Python and LTspice
Python code used for the RC circuit:





It's a nice post about RC circuit. It's really useful, I like it :). Thanks for sharing it.
ReplyDeleteThanks!
DeleteDear,good evening.
ReplyDeleteWhat´s will go the answer to linear circuit using ODE? See pic link
https://uploads.disquscdn.com/images/ea4864ccf49d79466dc5a583e5de1ef5fd900bff215f1e99c3403d78b69bcc18.png