This article is a follow up of the following:
Gradient descent algorithm
Here below you can find the multivariable, (2 variables version) of the gradient descent algorithm. You could easily add more variables. For sake of simplicity and for making it more intuitive I decided to post the 2 variables case. In fact, it would be quite challenging to plot functions with more than 2 arguments.
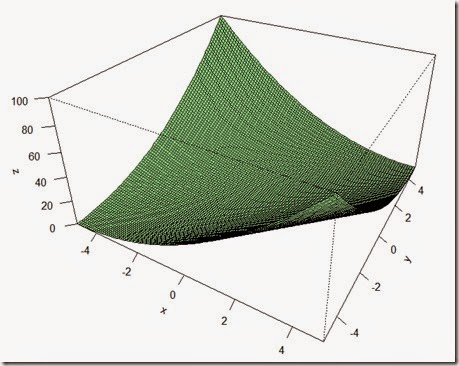
Say you have the function f(x,y) = x**2 + y**2 –2*x*y plotted below (check the bottom of the page for the code to plot the function in R):
Well in this case, we need to calculate two thetas in order to find the point (theta,theta1) such that f(theta,theta1) = minimum.
Here is the simple algorithm in Python to do this:
This function though is really well behaved, in fact, it has a minimum each time x = y. Furthermore, it has not got many different local minimum which could have been a problem. For instance, the function here below would have been harder to deal with.
Finally, note that the function I used in my example is again, convex.
For more information on gradient descent check out the wikipedia page here.
Hope this was useful and interesting.
R code to plot the function

Hey. Thanks for this amazing post. Most of the posts out there talk more on linear regression than 'gradient descent' itself. This is very well done.
ReplyDeleteThanks for reading! I'm glad you liked the post!
DeleteHow did you consider the value of theta and theta1 as 830 and 220?
DeleteThis is so helpful!!! BTW, what is "N" in "theta2 = theta - alpha*N(yprime.subs(x,theta)).evalf()"?(lines 29 and 30)
ReplyDeleteN is a function which evaluates an expression, i.e. converts the expression into an numerical value.
ReplyDeletehttps://docs.sympy.org/latest/modules/evalf.html
Thank you for sharing such a wonderful blog on RPA. I hope this information is very helpful for those who is searching for quality kmowledge on RPA. Surely this wonderful blog on RPA will help them .Requesting you to please update this blog on RPA time to time and help others.
ReplyDeleteThanks and Reagrds,
RPA training in chennai
best RPA training in chennai
RPA training cost in chennai
How did you consider the value of theta and theta1 as 830 and 220?
ReplyDeleteHi, Nice post. It very much clarified the concept.
ReplyDelete#modified code, without usage of sympy. 15 lines and 2 functions
Hi, Nice post. It very much clarified the concept.
#modified code, without usage of sympy, 15 lines and 2 functions.
# main function Fun1(x,z) = x**2 + z**2 - 2*x*z
def dFun1Bydx(x,z):
'''derivative with respct to x, keeping z constant'''
return 2*x -2*z
def dFun1Bydz(x,z):
'''derivative with respct to z, keeping x constant'''
return 2*z - 2*x
# Data
theta = 830 #x, an assumed value, you can take any
theta1 = 220 #z, an assumed value, you can take any
alpha = .01
for i in range(0,1000):
delta_x = dFun1Bydx(theta, theta1)
delta_z= dFun1Bydz(theta, theta1)
correction_x=alpha*delta_x #correction to x
correction_z=alpha*delta_z # correction to z
#print("delta x are",delta_x)
#print("delta z are",delta_z)
theta -= correction_x
theta1 -= correction_z
print("final x, z are", theta,theta1)
#result is
#final x, z are 525.0000000000014 524.9999999999986
#min value of function is 0.0