Gradient descent algorithm

Today I’m going to post a simple Python implementation of gradient descent, a first-order optimization algorithm. In Machine Learning this technique is pretty useful to find the values of the parameters you need. To do this I will use the module sympy, but you can also do it manually, if you do not have it.

The idea behind it is pretty simple. Imagine you have a function f(x) = x^2 and you want to find the value of x, let’s call it theta, such that f(theta) is the minimum value that f can assume. By iterating the following process a sufficient number of times, you can obtain the desired value of theta:

 

Now, for this method to work, and theta to converge to a value, some conditions must be met, namely:
-The function f must be convex
-The value of alpha must not be too large or too small, since in the first case you’ll end up with the value of theta diverging and in the latter you’ll approach the desired value really slowly
-Depending on the function f, the value of alpha can change significantly.

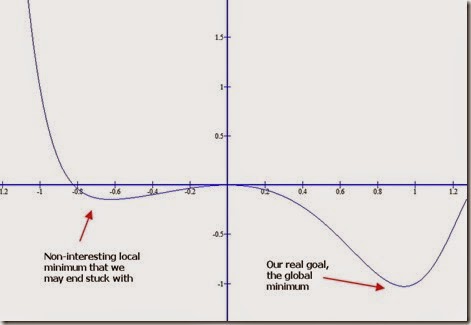
Note that, if the function has local minimums and not just an absolute minimum, this optimization algorithm may well end “trapped” in a local minimum and not find your desired global minimum. For the sake of argument, suppose the function below goes to infinity as x gets bigger and that the global minimum is somewhat near 1. With the algorithm presented here, you may well end up with x = –0.68 or something like that as an answer when you are looking roughly for x = 0.95.

In this case of course, it is trivial to find out the value and you don’t even need derivatives. However, for a different function it may not be that easy, furthermore for multivariable functions it may be even harder (in the next article I will cover multivariable functions).

Here is the Python code of my implementation of the algorithm

Hope this was interesting and useful.