Approximating differential equation with Euler’s method

It looks like it’s time for differential equations.

So, let’s say that you have a differential equation like the one below and you are striving trying to find an analytical solution. Chill out, maybe take a walk outside or ride your bike and calm down: sometimes an analytical solution does not exist. Some differential equations simply don’t have an analytical solution and might drive you mad trying to find it.

Fortunately, there is a method to find the answer you may need, or rather, an approximation of it. This approximation sometimes can be enough of a good answer.

While there are different methods to approximate a solution, I find Euler’s method quite easy to use and implement in Python. Furthermore, this method has just been explained by Sal from Khan Academy in a video on YouTube which is a great explanation in my opinion. You can find it here.

Here below is the differential equation we will be using:

and the solution (in this case it exists)

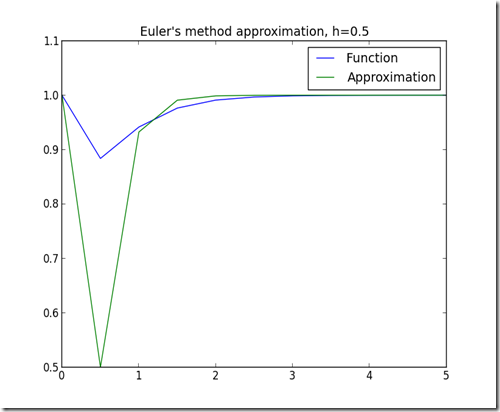
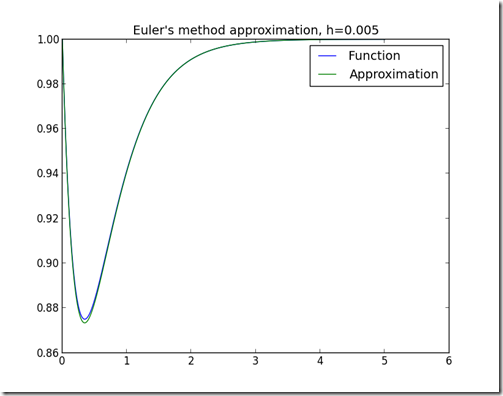
Here is the Python code algorithm. Note that the smaller the step (h), the better the approximation (although it may take longer).

Here are some approximations using different values of h:

Hope this was interesting.