Modelling a DC motor using LTspice, Simulink and Matlab

Electrically speaking, a permanent magnet DC motor can be modelled as follows:

applying LKT we obtain the following differential equation

$$v = Ri+L\frac{di}{dt}+e$$

where $R$ is the equivalent resistance of the brushes plus the windings, $L$ is the inductance as seen from the external terminals of the motor and $e$ is the back EMF. Usually R is very small and can be difficult to measure with a multimeter. The back EMF can be expressed as a function of the speed of the motor $e = k\phi\omega$.

Mechanically speaking, the motor can be modelled by considering the following equation:

$$J\frac{d\omega}{dt}=C_e-C_r=k_1\phi i - C_r(\omega)$$

The torque of the motor $C_e$ depends linearly with the current since the flux is constant (permanent magnet generate a constant flux). The opposing torque usually is constant, but in general may be a function of the angular speed of the rotor (think of friction for instance). If we put together these two differential equation, we find the following system:

$$\left\{\begin{matrix}
\frac{di}{dt} = -\frac{R}{L}i- \frac{k \phi}{L}\omega + \frac{v}{L}
\\
\frac{d\omega}{dt}=\frac{k_1\phi}{J}i - \frac{C_r(\omega)}{J}
\end{matrix}\right.$$

then, assuming the relationship between $C_r$ and $\omega$ is linear, the following system can be built

$$\frac{d}{dt}\begin{pmatrix}
i
\\
\omega
\end{pmatrix}=\begin{pmatrix}
-\frac{R}L{} & -\frac{k \phi}{L}\\
\frac{k_1 \phi}{J} & -k_f
\end{pmatrix}
\begin{pmatrix}
i
\\
\omega
\end{pmatrix} + \begin{pmatrix}
\frac{v}{L}
\\
-C_{r_0}
\end{pmatrix}$$

The variable of interest is the angular speed of the motor, therefore

$$y = \begin{pmatrix}
0 & 1
\end{pmatrix}\begin{pmatrix}
  i
\\
  \omega
  \end{pmatrix}= \omega$$

Now the system has been transformed in the canonical state

$$\frac{d}{dt}\bar{x} = \bar{A} \bar{x}+ \bar{B}\bar{u}$$

$$\bar{y} = \bar{C}\bar{x} + \bar{D}\bar{u}$$

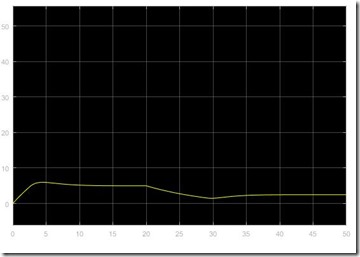
Using Matlab we can simulate the system response to a unit voltage step. Note that I’m assuming the torque of the mechanical load is constant in this case.

As you can see in the comments in the code, the final state of the system can be calculated just by setting every derivative to zero and then solving for the state variables. In this case it turns out that by applying a unit voltage step, the motor is absorbing 0.2 A and turning at a speed of 45.8 rad/s. You can take a look at the transient of the angular speed variable in the graph below

This is a nice result but we can’t really control the motor. I mean, we can vary the voltage and then get a certain speed as output but in most cases we need a certain speed regardless of the voltage (provided it is within the nominal voltage). In the second part of the code, I decided to put a PI regulator in series with the system and then use negative feedback to control the speed of the motor. Now we can set as an input a certain speed and see how the motor behaves in the transient. By requiring the motor to reach a speed of 1 rad/s, this is the transient that follows:

You can immediately notice that the motor took less time to get up to the required speed compared to the previous case. Why is this happeing? This is happening because by inserting a regulator and negative feedback the poles of the system (and therefore its dynamic behaviour) have been changed.

Modelling a DC motor with Simulink

Simulink, quote, “is a graphical programming environment for modeling, simulating and analyzing multidomain dynamic systems”. Simulink was made for simulating dynamic systems and it is particularly useful whenever you need to simulate models described by differential equations. You may, legitimately, ask why use Simulink? A DC motor is very simple, I can use other tools or even just pen and paper to find out the solution to my questions. I think the advantage of using Simulink is that it allows you to simulate different scenarios and complex models in a very short time. In our example we are simulating a DC motor, but think of a parallel of synchronous generatos, what if you’d like to simulate what happens in case of a short circuit at a specific point in a branch of the transmission line? Let’s see some more interesting simulations on the DC motor. The raw model of the DC motor can be modelled as follows

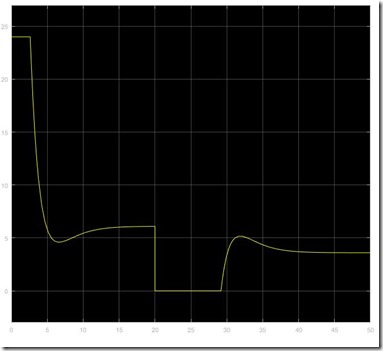
The model can then be wrapped in a subsystem and then used within other models. For example, let’s simulate a short circuit. In the following example the motor is started at time 0 with a 24 V step. At 60 seconds, a short circuit happens, the voltage on the motor terminals becomes zero. What would you expect the current to do? Let’s find out. We apply a 24 V step voltage to the motor, let it reach the equilibrium and then apply a short circuit! This is the Simulink model

If we take a look at the first scope, we find out that the current has the following behaviour:

Current as a function of time [A]

Note that initially the current is limited only by the resistance of the windings which is very low, therefore a big current spike of about 4.36 A (which is exactly equal to 24V /  5.5 Ohms) follows the application of the voltage. If you were powering this motor directly from a solar panel for instance, you might run into trouble at the startup since the panel may not be able to supply the current required at startup. Batteries can usually do that but always check the data sheet to be sure. Then, as the speed increases, the back EMF increases as well reducing the current through the windings. For everyone that is familiar with RL circuits, this overall behaviour might seem odd at a first glance: at 60 seconds the short circuit occurs and the current seems to jump immediately to a minimum negative value. However, if we zoom in the milliseconds range, we can easily find out the typical behaviour of an RL circuit. The current changes accordingly to the time constant of the motor which is about 0.5 ms. This means that the current will be practically constant after about 2 ms. This is exactly the behaviour we find out in the graph below.

 

Detail of the current behaviour in the millisecond time scale [A]

What is the reason behind this behaviour? The first graph shows the current’s behaviour for times much larger than the L/R time constant. Since the mechanical time constant is much larger than the electrical one (the mechanical time constant should be about 10 seconds, judging from the graph) in the first milliseconds of the transient, we could assume that the angular speed is constant and neglect completely the mechanical behaviour. Another interesting thing to notice is that when the short circuit happens the current becomes negative, this means that the current starts to flow in the opposite direction. This is understandable since now there is nothing opposing the back EMF which depends only on the angular speed. If you look closely at the end of the transient, the current becomes positive again: since the resistant torque is supposed constant, when the motor reaches a speed of zero, it continues to accelerate until the electromagnetic torque equals the resistant torque (0.1 Nm). The back EMF changes sign (it becomes negative) and therefore the current changes sign as well (it becomes positive again). In practice this behaviour can be found, for example, in a DC motor used for pulling an object up to a structure. As soon as the short circuit happens the force of gravity pulls the object back to earth and the “resistant torque” applied is almost constant. This is obviously not the case of an electric motor of a car: in that case the motor will simply stop due to friction and other losses which basically depend, to some extent, on the speed.

In our example, at the equilibrium after the short circuit, the current is 0.2 A and the speed is 2.2 rad/s (in the opposite direction with respect to the initial speed). The terminals of the motor are shorted, no current is pumped into the supply, but the mechanical load is supplying 0.1 * 2.2 = 0.22 W of power. Where is that power going? Simple, it is being dissipated as heat by the windings since 5.5 * 0.2^2 = 0.22 W exactly as expected.

Controlling the motor with a PI controller in Simulink

What if we’d like to control the motor speed directly as we did in the Matlab code in the introduction? Well we’ll just implement the control loop in Simulink then:

Note that:

1. A PI controller has been connected in series to the system. The PI controller takes as input the error (the difference between the set point and the actual angular speed) and outputs the voltage to apply to the motor.
2. In order to make the simulation more realistic, the output of the PI regulator has been constrained to the 0-24V range.
3. The set point changes as follows: at time 0s the set point equals 10 rad/s, at time 20s it jumps to 5 rad/s.

If we take a look at the physical quantities we find the following behaviour:

Angular speed [rad/s]

Back EMF [V]

Current [A]

As you can see from the first graph, the system is now much quicker in its response, the equilibrium is reached in about 15 seconds (previously, 60 seconds were needed). This increase of response time, however, is characterized by a bit of overshoot, in fact the speed exceeds the set point and then gets back to it. This can be avoided by fine tuning the PI controller further. This overshoot is reflected in the current’s behaviour.

PID: actual applied output voltage [V]

PID: theoretical applied voltage [V]

Perhaps the output of the PI controller is more interesting. Initially, and at the time the set point is changed, the PI controller would like to apply a very high voltage, as high as about 55 V. Assuming the supply is capable of applying such a voltage, this could damage the motor, a saturation block is used to prevent this problem.

Adding a PWM control to the control loop

It is often the case that many hobby projects use PWM control for DC motors. Say no more, we can simply add a PWM block to our simulation. Well, in this case the “simply” part is not true. I had to think a bit on how to make this subsystem, but it was worth it. The PWM subsystem is shown below above the new control loop

PWM Subsystem

Control loop of a DC motor with a PI controller and PWM

The angular speed seems smooth as you would expect, while the PWM output is fine except that it is, obviously, a bit messy to look at

Angular speed [rad/s]

PWM voltage applied to the motor [V]

I hope you enjoyed this overview of control loops and DC motors. I had these models in my computer for a long time. You can download all the Simulink files here if you wish to tweak and tinkle with them.