Another typical control problem: balancing a ball on a beam

Balancing a ball on a beam is not a common problem you may face during your everyday life, however, this simple example of engineering can be extended to more complex problems and, in general, to other more interesting control problems such as

• Control of temperature in a room
• Control of robots
• Control of automated cars
• Control of industrial processes

The main problem tackled in this article is the design and implementation of a basic PID based controller to control the position of a ping pong ball on a beam. Ideally the controller should be able to set the position to whatever value of the x axis the user decides to apply. This is a simple scheme of the physical system

The aim of the project is to design a digital controller that can set the position of the ping pong ball and reject noise. I am going to use a controller of the PID family since it is simple and widely used in the industry.

The physical system

First of all comes the study of the physical system. The problem can be generalized to other dimensions however, for the sake of simplicity it is limited to one spatial dimension. Note that we are using a rotating reference frame which is joint to the moving stick. Below is the sketch of the free body diagram:

As you can see, there is basically only gravity as major force at play, the other forces will be used to write down the equations needed to determine the relationship between the angle of the support and the acceleration of the ball.

At this point, we can label our variables as follows:

1. The **controlled variable** is the $x$ position of the ball.
2. The **control variable** is the angle of the stick $\theta$. This is going to be the variable directly affected by the controller through the servomotor.

We can now write the equilibrium equations for the ball and solve for the acceleration

$$
\left\{\begin{matrix}
N - mg\cos \theta = 0
\\
mg\sin \theta + m\ddot{x} + T = 0
\\
RT - J_d \dot{\omega_d} = 0
\end{matrix}\right.
$$

where:

the angular velocity:
$$\dot{\omega_d} = \ddot{\theta} = \frac{\ddot{x}}{R}$$

$J_d$ is the moment of inertia of the ball (which has no mass inside of it):
$$J_d = \frac{2}{5}mR^2$$

By solving the equation we find out that the acceleration on the x axis is equal to:

$$\ddot{x} = -\frac{5}{7}g\sin \theta$$

Now we need to approximate theta since the $\sin$ function is not very manageable.
For small $\theta$, angles we can approximate $\sin theta$ to be equal to $\theta$. This approximation is usually good, however, we might want to remember this when designing the controller later.

The continuous transfer function of the system

The continuous transfer function of the system can be found by applying the Laplace transform to both sides of the last equation and dividing the output variable by the input variable:

$$s^2 X(s) = \frac{5}{7} g \Theta (s)$$

$$\frac{X(s)}{\Theta(s)} = G(s) = \frac{5}{7}g\frac{1}{s^2} = \frac{k}{s^2}$$

We ended up with a very simple transfer function with two poles in the origin. This function can be studied in MATLAB although it is not that interesting:

Finding the appropriate controller in a closed loop

By putting the transfer function in a closed negative feedback loop we need a controller to be used to steer our system towards the desired goal.

The system, on its own, is unstable. A controller is needed. Since there are already two poles in the origin, without a controller (ie with R(s) = 1) the phase margin is zero and the system is unstable. While a proportional controller is not enough and a PI controller would worsen the problems, a PD controller is perfect for the task at hand. A pure PD controller though does not exist in practice therefore, an approximated version is needed:

$$ R(s) = k_p + D \frac{N}{1+\frac{N}{s}}$$

The closed loop function $L(s) = N(s)/D(s)$ becomes

$$L(s) = R(s)G(s)

Since the transfer function from $\theta$ to $x$ in a closed loop is given by $\frac{L(s)}{1+L(s)}$ The closed loop poles are given by the following equation

$$1 + L(s) = N(s) + D(s) = 0$$

The closed loop poles depend on the parameters of the controller. We can now tweak those parameters in order to modify the response of the system. By using the *pidTuner* function in MATLAB you can easily choose the best parameters according to the needs of your project. The pidTuner function is awesome since it lets you easily visualize crucial parameters such as overshoot, rise time and settling time.

In this case, the following values were chosen: $k_p = 0.38$, $D=0.5$ and $N=50$.

It is possible to calculate the phase margin directly by using the margin function in MATLAB:

the phase margin appears to be about 73 degrees which is nice to see. The gain of the system is 1 as expected and confirmed by the step response:

The root locus shows how poles move in the complex plane by varying the gain of the closed loop function from 0 to infinity:

As the gain tends to infinity, the closed loop poles tend to the zeros of the closed loop function (or infinity if there are less poles than zeros). Note that the zero of the controller is exactly -9.09 which is also a zero of the L function.

Simulink, a nice shortcut to model a system and design a controller

Using Simulink, one could have avoided most of the trouble of simplifying the system or why not compare the simplified and the complete system. Below you can find the schematics of the complete system. The minus sign in the transfer function of the system is needed since I switched the x axis.

Detail of the Subsystem modelling the physical system

Complete Simulink schematics

Note that a saturation bloc is needed since it is probably best to limit the output of the PD controller. In case that the simplified system is used, a saturation bloc is needed to ensure that $\theta < \frac{\pi}{6}$. It is worth noting that by limiting $\theta$, the differences between the simplified and the complete model are very small if noticeable at all.

Tuning of the controller can be done directly within Simulink

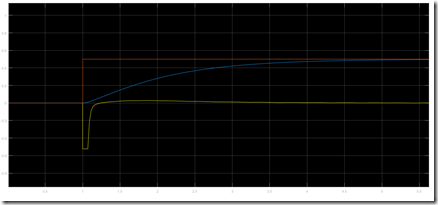
The results of the simulation are displayed in the graph below

In orange is displayed the set point, in blue the position on the x axis of the ball and in yellow the output of the PD controller (in radians). The settling time is about 4 seconds.

Note that the output of the PD controller has been restrained

PD output

How would I go to make such controller though?

Well, an old school option is to use old fashioned op amps!

You can find the Simulink and LTspice files here. I hope you enjoyed this article! Have fun!