Three-phase symmetric perfectly balanced system LTspice simulation

A symmetric, three-phase and perfectly balanced system can be easily modelled either by pen and paper with the use of phasors or using LTspice which is faster. In case you would like to try I suggest to first try the pen and paper way and then check the results on the simulator. A basic example of such system would be the following:



The main characteristics of a three-phase system is that each conductor carries an AC current with the same frequency and amplitude. This can be modelled by placing three voltage generators as in the picture above.

Voltage source settings

As you can see I chose the voltage source to output a sine wave shaped voltage.
The first non-zero values indicates the maximum voltage value which is about $\sqrt(2) 220 V$ since our system is symmetric. As far as the frequency is concerned, industrial frequency in the EU is 50-60 Hz (I set 50 Hz), finally each voltage source has a phase shift of 120 degrees with respect to the “upper one”.

Load characteristics

Since the system is balanced, every load on each line should be the same. I decided to add an inductive component to the resistive one represented by 100 Ohm resistors. Since the reactance has a prevalent inductive component I expect the voltage to lag behind the current by 90 degree. Just by comparison I suggest you to try and replace the inductors with capacitors.
The transient simulation should be fine and around 100ms should suffice for this example. By clicking “run” I can start making some interesting observations:

Observations

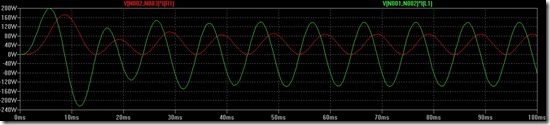
First of all as you can see by the picture below, the three currents have the same amplitude and frequency but they are shifted by 120 degrees each. This should not be a surprise since we built our system this way. Secondly, it is worth noting that by making our assumptions about the symmetry and the load being balanced, we can avoid analysing all the three phases and concentrate our attention on a single one (the others will be the same but shifted).



Another important point to note is that since the impedances are all equal, and the system is symmetric, the voltage between the two ends of the system is zero! This massively simplifies the analysis of the circuit.



And, as expected, the voltage lags behind the current in each phase. This is due to the fact that the impedances have a strong inductive component (they are inductors). Be careful to remember they are measured in different units of measure since current and voltage are different! Sometimes this feature of LTspice that lets you plot two different physical quantities in the same plot may be misleading.



As far as power consumption is concerned, by pressing “alt” before clicking on a circuital element you can plot the electric power as a function of time. As you can see below, the resistor absorb a non zero power on average, to be precise it is around 49 W, while the inductor since it is ideal with no internal resistance it is only capable of accumulating and releasing energy, therefore it does not absorb any real power on average (you can calculate reactive power though!)

A little side note: variable frequency simulation

As a little side note, you should note that as frequency increases, the current flowing through the impedance goes down. This is again to be expected since the inductor needs time to let current flow through it, so intuitively one can expect that if we “switch the current” on and off faster and faster (.i.e raise the frequency) as frequency tends to infinity the inductor will not let any current through it. We can simulate this behaviour using a variable parameter and a spice directive

By entering the .STEP directive I simulated the circuit behaviour at a frequency of 50 and 10050 Hz. As you can see at a higher frequency the current is near to zero. By zooming in you can actually see that some current is however still flowing, since to actually achieve a current of zero we would have to set the frequency to an infinite value (all other parameters being equal and constant).
You can download the LTspice schematics from here.