Crankshaft connecting rod and piston mechanism simulation with Python

What is a crankshaft connecting rod and piston mechanism? It basically is a mechanical part which converts rotational motion into reciprocating motion. The applications are pretty vast, car engines are one of the most obvious I can recall right now.
It turns out the physics behind this mechanism is pretty interesting and easy to code, therefore I thought I could give it a go and try to make a simulation.
First of all we need to define the problem and solve it:



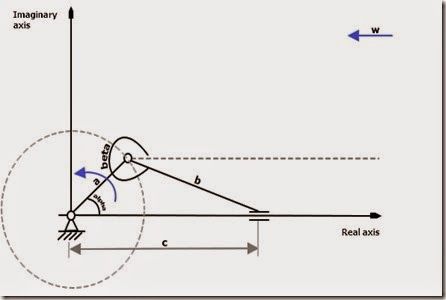
This is the basics from which we start: the crankshaft (rod ‘a’), the connecting rod (rod ‘b’) and the piston whose position is denoted with c. The motion of rod ‘a’ is a pure rotational motion while the motion of rod ‘b’ is somewhat more complex. The piston is performing a linear motion since it is constrained onto the real axis.
Now you might ask yourself why I am using the imaginary plane… It turns out that you can represent each vector (a,b and c) with a complex number, and this semplifies our problem into a more manageable system of two equations.
By using vector properties we can easily write:

The vector equation above states that the position of c is the sum of a and b as it can easily be seen on the picture. Now, we can get our real and imaginary coordinates in the plane by using Euler’s formula:

Note that every one of these parameters is a function of time and assuming that alpha(t), the length of the rods a and b are known, the system can be solved for c and beta. Furthermore by deriving the original equation we can obtain velocity and acceleration for each time t, since assuming alpha(t) is known then the derivatives of alpha(t) are known too (assuming alpha is derivable two times with respect to t).
Here are velocity and acceleration (vectors), respectively:


Now, for the sake of this example, I am assuming  however that’s not necessary. For instance one could try angular acceleration constant and so on.
Given my assumption, is known and the initial angle can be assumed later. Now we can solve our first system for and . The solution looks something like this:


Ok, so far so good, now that we have the position at each time we just need to translate everything in a language that Python can understand: I used a class, however you can easily avoid using it since it is not really necessary


Once we have coded all what is above, we can create a My_mechanism instance and call the methods, be sure not to call all the methods at once since it will not run them all. Call a method at each time:

Here below are the videos I made using the animations of the mechanism:

 

 

Hope this was interesting.