Suppose you have a sample of your data, maybe even a large sample, and you want to draw some conclusions based on its probability density function. Well, assuming the data is normally distributed, a basic thing to do is to estimate mean and standard deviation, since to fit a normal distribution those two are the only parameters you need.
However, sometimes you might not be that happy with the fitting results. That might be because your sample does not looks exactly bell shaped and you are wondering what would happened if the simulation you ran had taken this fact into account.
For instance, take stock returns, we know they are not normally distributed furthermore there is the “fat tails” problem to take into account. At least it would be interesting estimate a probability density function and then compare it to the parametric pdf you used before.
Here below is a simple example of how I estimated the pdf of a random variable using gaussian_kde from scipy
and here is the plot that we get
What we can see is that the estimated pdf is “more dense” around the mean and has some more density on the tails.
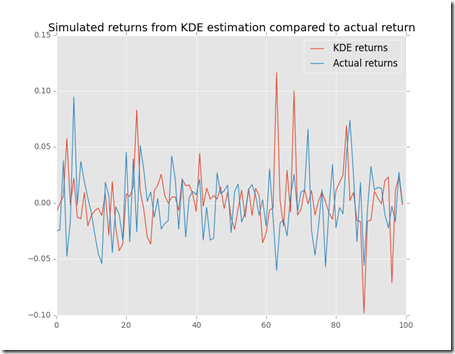
Let’s use this data to simulate a sample
For sure in this randomly generated sample there are some extreme values and they look close to the actual sample.
Hope this was interesting and useful.
Disclaimer
This article is for educational purpose only. The author is not responsible for any consequence or loss due to inappropriate use. The article may well contain mistakes and errors. The numbers used might not be accurate. You should never use this article for purposes different from the educational one.

Thanks. It's a nice post about probability density function. I really like it :). It's really helpful. Good job.
ReplyDeleteCan probability density function take values greater than 1?
ReplyDeleteWhere is the data file?
ReplyDeletewhats the format of the data file?
ReplyDeleteThis comment has been removed by the author.
ReplyDelete
ReplyDeleteThis is a great inspiring blog.You have shared really very helpful information thank you.
Data Scientist Course in Jaipur
Very informative message! There is so much information here that can help me thank you for sharing
ReplyDeleteData Analytics Course in Lucknow
I couldn't leave your website until I told you that I really appreciated the high quality information it presents to your visitors. I will come back frequently to check for new posts.
ReplyDeleteData Scientist Course in Durgapur
I enjoyed reading your articles. I have bookmarked it and I am looking forward to reading new articles. Thanks for sharing.
ReplyDeleteData Science Course in Ahmedabad
Thank you for your message. I've been thinking about writing a very similar article for the last few weeks, I'll probably keep it short and to the point and link to this article instead if that's interesting. Thank you.
ReplyDeleteBusiness Analytics Course in Ernakulam
Great blog! The explanation of how to estimate the probability density function using Python was really clear and easy to follow.
ReplyDeleteAlso Read: How Cloud and Edge Computing are Transforming Software Testing