Fourier series is one of the most intriguing series I have met so far in mathematics. Roughly speaking it is a way to represent a periodic function using combinations of sines and cosines. There are many other fascinating topics such as the Laplace and Fourier transforms but I am new to complex analysis and techniques so I’ll go step by step!
There are many reasons why I find Fourier series fascinating but primarily, I like the fact of approximating functions using the sines, cosines and complex exponentials because of the bond between these functions.
Now, what are the ingredients we need to approximate a function with a Fourier series?
1) A periodic bounded function, with period T
2) The function should be integrable over the period
If the above conditions are met, then we can write the function as follows
Note that this is an infinite sum, the more terms you add, better the approximation. As far as the coefficients are concerned, you can calculate them using the formulas below.
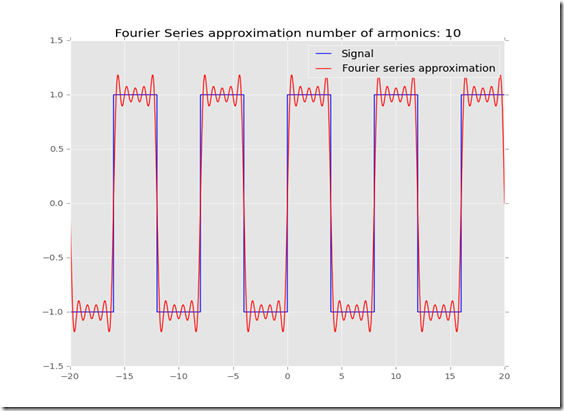
For this simple test, I chose the square wave function, which could be interpreted as an on and off signal. The aim of this simple test was to check how good is the approximation. Using only 10 armonics (n=10) this is the result I got:
I would say it is pretty accurate, Python took only a few seconds to calculate it. Furthermore you can use more complex periodic functions and found similar amazing results. Here are some useful resources I used:
http://en.wikipedia.org/wiki/Fourier_series
http://en.wikipedia.org/wiki/Square_wave
If you have time, perhaps you could try plot the sawtooth wave
In the square wave Wikipedia page there are other kind of wave functions, perhaps in the future I’ll try them out too. Below is the Python code I used to plot the square wave.
Enjoy!
![clip_image002[14] clip_image002[14]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhGPuYqhMv3dz2hVrutZ9QBp-Z964XprS4ps1rzLOMwh_rNkuezQFZUgccd5dQSSCd-eXfFMFd7-Ko3OVHJXoIfP2bj7Z4YLGtOn6GQe8LW53phd-gHgIYsuQCToPZAns981No7s7Yykl0/?imgmax=800)


What is "n_max" in the code given above for square wave approximation
ReplyDeleteHi, n_max is the number of harmonics used.
DeleteThis comment has been removed by the author.
ReplyDeleteHi there!
ReplyDeleteGood stuff, thank you!
I'm currently learning to translate mathematical notation to working algorithms for my master's thesis, so your code was a first step and a huge help.
Just one question that came up though: If you cycle from 1 to 10 in line 56, don't you get 9 harmonics instead of 10? Not trying to be a smartass here btw, I'm just trying to grasp this.. ^^
And I'll definitely remember the modulo trick from line 41, too. ;-)
You get 9 armonics in the cycle but before you have got a0, so it's 10 armonics in total.
DeleteThis make my eyes bleed:
ReplyDeleteif one == 1:
one = -1
negativeOne = 1
else:
one = 1
negativeOne = -1
I used your code, but I wrote a shorter square wave function that handles the discontinuities more consistently (unless I missed something):
ReplyDeletedef squareWave(x):
global T
x=x/(T/2)
if math.remainder(math.ceil(x),2):
return 1
else:
return -1
This comment has been removed by the author.
ReplyDeletecould someone help me with the code for f(t) = t^2+2t+3 please?
ReplyDelete