Markets, stocks simulations and Markov chains

This article is some sort of continuation from this one.

Our previous model for stock simulations did not take in account the following idea:
when a stock (or the market) is going up, then it should be (intuitively) at least, more likely that it will continue to go up. Or at the very least, as it is the case for a football game, it does not feel right to believe that the probability of either of the two possible outcomes is exactly 50%.

The idea behind Markov chains is really versatile, we can apply it also to the markets.
With a “bit” of study (I’m being sarcastic here), you can come up with something pretty complicated like this, however, the model I’m going to show here is much more naive and easier.

Suppose a Markov chain with two states, market up and market down. Once you found the probabilities of each state, you can easily simulate a random walk (based on a Markov chain of course).

Here is the code for this model:

The graphs below represent respectively, 2, 200 and 500 random paths.

2 random walks

200 random walks

500 random walks

Hope this was interesting.

---

Disclaimer
This article is for educational purpose only. The numbers are invented. The author is not responsible for any consequence or loss due to inappropriate use. It may contain mistakes and errors. You should never use this article for purposes different from the educational one.

A first really shy approach to Machine Learning using Python

The day before yesterday I came across Machine Learning: WOW… I got stuck at my pc for an hour wondering about and watching the real applications of this great subject.

I was getting really excited! Then, after an inspiring vide on YouTube, I decided it was time to act. My fingers wanted desperately to type some “smart” code so I decided to write a program which could  recognize the language into which a given text is written.

I do not know if this is actually a very primitive kind of Machine Learning program (I somehow doubt it) therefore I apologize to all those who know more on the subject but let me dream for now.

Remember the article on letter frequency distribution across different languages?? Back then I knew it would be useful again (although I did not know for what)!! If you would like to check it out or refresh your memory, here it is.

Name of the program: Match text to language

This simple program aims to be an algorithm able to distinguish
written text by recognizing what language a text
was written in.

The underlying hypothesis of this model are the following:
1. Each language has a given characters distribution which is different from the others. Characters distributions are generated by choosing randomly Wikipedia pages in each language.
2. Shorter sentences are more likely to contain common words that uncommon one.

The first approach to build a program able to do such a task was to build a character distribution for each of the languages used using the code in the frequency article. Next, given a string, (sentence) the program should be able to guess the language by comparing the characters distribution in the sentence with the actual distributions of the languages.

This approach, for sentences longer than 400 characters seems to work fine. However, if the sentence were to be shorter than 400 characters, a mismatch might occur. In order to avoid this, I have devised a naive approach: the shorter the sentence, the more likely the words in it are the most common. Therefore, for each language,a list of 50 most common words has been loaded and is used to double check the first guess based on the character frequency only in case the length of the sentence is less than a given number of characters (usually 400).

Note that this version of the program assumes that each language distribution has already been generated, stored in .txt format and it simply loads it from a folder. You can find and download the distributions here.

So far the program seem to work on text of different length. Here below are some results:

In these first two examples I used bigger sample sentences

In this last example, the sentence was really short, it was just 37 characters, something like: “Diese ist eine schoene Satze auf Deutsch”. In this case it was hard to draw a distribution which could match the German one. In fact the program found French and was really far away from the right answer indeed. The double-check algorithm kicked in the right answer (Lang checked).

Hope this was interesting.

Weather forecast through Markov chains and Python

A Markov chain is a mathematical system that undergoes transitions from one state to another on a state space. It is essentially a kind of random process without any memory. This last statement, emphasizes the idea behind this process: “The future is independent from the past given the present”. In short, we could say that, the next step of our random process depends only on the very last step occurred. (Note that we are operating in discrete time in this case).

Let’s say that we would like to build a statistical model to forecast the weather. In this case, our state space, for the sake of simplicity, will contain only 2 states: bad weather (cloudy) and good weather (sunny). Let’s suppose that we have made some calculations and found out that tomorrow’s weather somehow relies on today’s weather, according  to the matrix below. Note that P(A|B) is the probability of A given B.

 

Therefore, if today’s weather is sunny, there is a P(Su|Su) chance that tomorrow will also be sunny, and a P(C|Su) chance that it will be Cloudy. Note that the two probabilities must add to 1.

Let’s code this system in Python:

Obviously the real weather forecast models are much more complicated than this one, however Markov chains are used in a very large variety of areas and weather forecast is one on them. Other real world applications include:
-Machine learning (in general)
-Speech recognition and completion
-Algorithmic music composition
-Stock market and Economics and Finance in general

For more information on Markov chains, check out the Wikipedia page.

If you are interested in Markov chains, I suggest you to check these two video series on YouTube which are (in my opinion) good explanations of the subject.
-Brandon Foltz’s Finite Math playlist, very clear explanation with real world examples and the math used is fairly simple. You just need to know a bit of matrices, operations on matrices and probability (but if you are here I guess you have no problems on this)
-Mathematicalmonk’s playlist on Machine Learning, where a more technical (formal) explanation is given in the videos on Markov chains, starting from here.

Hope this was interesting and useful.
-

Arduino module GUI (Beta version)

Hi everyone! I have just completed a first, very basic GUI to get the Aduino module (which by the way you can find here) more user friendly.

The GUI is still a “Beta” version since I have created it with PyQt4 which I started learning only 3 days ago. I bet there are plenty of features which could be improved. I am probably going to revise and update this GUI, however here is a first “raw” version which, as far as the connection and communication with Arduino Uno is concerned, works fine.

This application is for educational purpose only, any commercial purpose is excluded.

You can download the executable for windows here. For Mac and Linux users, the source code is included in the zip folder however I am not sure the program will work since I have no experience with those operating system and their USB settings. Feedbacks are much appreciated.

Here are some screenshots and some useful information:

This is the main screen. The three buttons at the bottom essentially sum up everything that this program should help you doing.

First of all, you need to connect Arduino Uno to the USB port and load your program in.
Then you can click on connection on your GUI and click “Set up connection”. The default port is com3 and 9600 baud. You can easily change these default settings in the connection menu available in the GUI.

Once the connection has been established you can start interact with Arduino Uno.

By clicking on the button “Read from Arduino” the program asks you how many lines to read, there’s still no default values however I suggest to read not more than 100 lines since the program might slow down or crash.

By clicking on the button “Send to Arduino”, the program asks you to enter the data to send. You can enter one of the three data types showed below in the following form:
1. Integer: 2
2. Character: b
3. List: [2,3,4,5,6,7,8]

The list can be as long as you want it to be.

Hope this is useful.

Controlling your Arduino Uno board with Python

Today I am going to talk about a particular topic which overlaps Arduino and computer programming.

Last month I was watching video about electronics and thinking about the solar controller which many solar stand alone kits use. For some reason they do not behave as they should (i.e. cut the power to the lights when the sun is rising and give full power in the evening). However, a far more important point is that for this kind of controller a centralized control system is not available. Therefore I had a great idea: let’s try to program a board such as Arduino, to do the job.

I bought an Arduino Uno, the basic model, which I guess is suitable for beginners as myself. You can check more details here.

Arduino is an open source project and can be programmed in a language which is similar to C. This point is fine, since I have some knowledge of C and can get by quite easily with beginner projects. Once the main code has been loaded on Arduino, you can interact with the board through the USB and the “shell”, and, for instance, give instructions to trigger some control flow structure such as if-if else- else. However, in some cases it does not work (still do not know why) or it is impractical, since you can enter only one value at time. It would be nice to control the board with some external tool which could let you write some script to execute. It turns out that there is a module which enables you to do such operations. This module is pySerial. It can be downloaded here and is available for Python 3 as well!

The module is great! It works really smooth and in a linear manner, as it should. However, Arduino accepts only raw bytes and binary code as input therefore some little amendments must be made to be able to communicate with it through Python 3. Note that there are some differences with Python 2 which I will not cover.

First of all, Python 3 wants naturally work with ASCII characters, therefore when sending an integer to Arduino Uno, our sweet board will understand anything but what we have sent. For characters such as ‘a’, the matter is somewhat at ease, since you just need to send the character with a b in front of it: b’a’. On the opposite side, when reading data, you need to convert it into a readable format. To solve all these “problems” I decided to build a simple class which essentially is a wrapper of some functions of Serial and can be used directly to send characters, lists and integers to Python. Perhaps I will add also the possibility to send floats and strings although I am not sure the latter can be send and understood from the board.

Here is a basic example of communication with Arduino Uno through Python 3.

First of all we need to load the following code to Arduino Uno. This simple code lights a LED light according to the value of  readData which is read from the USB port. Serial.print prints out the value of readData to the USB port.

For instance, to control the board in this case, you can use this Python code:

However, writing this code again and again is boring and can easily lead to mistakes. Therefore I decided to built a class whose name is Arduino

By creating an Arduino object using the ArduinoClass, you can call the following methods:

I am also working on a GUI with PyQt4 for this script. I will keep you posted.

The source code of the ArduinoClass is available here.

Hope this is useful!

(Naive) RSA encryption with Python

Please before continue reading, make sure to read the disclaimer at the bottom of this article.

RSA is a well-known cryptosystem used in many cases where secure data transmission is needed. It basically rely on the also well-known issue of factoring big numbers. As you may recall from high school, each number has a unique prime number factorization. This is the very strength of RSA. In order to decrypt a message encrypted with RSA you would need to factorize a REALLY BIG number and this problem may take a very long time to be solved, it may take so long that it becomes unpractical to be achieved.

If you want to get more on RSA click here.
Here is the algorithm carefully described.

I have always been fascinated by encryption and cryptosystems. For those who did not know, Alan Turing, during the Second World War, devised a machine which made it possible to decrypt Enigma code in relatively short time and therefore gain a significant advantage. This machine was basically the first computer. You can watch this incredible piece of history on you tube. Here are some interesting videos:

Numberphile Enigma video
An interesting documentary

Now let’s get to the necessary premises and the code!
First of all, to start off you need two big primes, p and q. I do not know how they usually get these primes (I haven’t covered it yet) but anyway, they are almost all you need to start your “naive” RSA encrypting system in Python. We will use small numbers for the sake of simplicity and this is basically one of the factors that led me to use the word “naive” since it could be easily broken in a short time.

Here is the result which should be printed out:

Therefore, hypothetically, Bob, who needs to send a message (512) to Alice, would use Alice’s public key to encrypt 512 and then send her the number 477. Alice would then use her private key to decrypt 477 and get back 512, the original message.

Hope this was interesting.

---

Disclaimer: This article is for educational purpose ONLY. If you need a security system you should ask to professionals who are competent in the field. The author of the article is by no means a professional or an expert in this field and might, therefore, make big mistakes. This code must NOT be used for anything other than educational purpose. The provider of this code does not guarantee the accuracy of the results and accepts no liability for any loss or damage that may occur as a result of the use of this code. Understanding and agreeing to the terms of this disclaimer is a condition of use of this code. By reading the article you confirm you have understood and will comply with this disclaimer.

Plain vanilla BlackJack simulation with R

Please before continue reading, make sure to read the disclaimer at the bottom of this article.

Here is a simulation I run with R in the same period I created the poker one.

I have just decided to call it plain vanilla since neither double down or split pairs are allowed. Rules are as basic as they can be.

The code looks like messy, I know, If I had to do it now, I guess I would do many things differently, however, the results looks fine, and the code runs fine as well, therefore it is not entirely to be thrown away I believe.

The simulation is divided in two parts. In the first one I looked for the probabilities for each possible event (that’s to say: “player wins”, “tie”, “dealer wins”). Since the code looks pretty hairy, many explanations are provided.

A small but important note: if you want to run the simulation, since it is a bit demanding computationally speaking, in order not to crash RStudio you may want to run a line a time and not the entire code all at once, or just maybe use only some functions, just be careful because since we run the simulation a big number of times and the functions are not the fastest to be run, your computer might complain a little.

Here is the code:

Let’s have a look at the results that we have got:

By simply standing with a hand equal to 19, you can expect to win 59% of the times, and loose 28%. A tie is likely to occur 13% of the times.

Let’s now simulate 2000*100 games with a hand equal to 18 and 3 decks and then average the probabilities:

In this case the odds seem to be a lot worse than before, by just subtracting 1 point to the player’s hand we raised the probability of win for the dealer from 28% to 43.4%.

Why not run the simulation for each hand from 16 to 21 and then plot the results? Warning: your computer may yell at you after this demanding step!

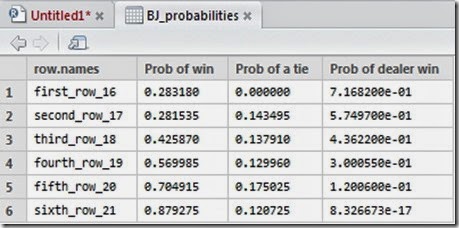
As we could expect, as the player’s hand gets higher, the probabilities of winning increases. For some reason which I ignore, R did not print in plain the probabilities of winning for the dealer, however you can easily get them from the table above or by calculating for each row 1 - Prob of Win – Prob of a tie, since the three events should (must) sum up to one. It is interesting to note that the probability of a tie is more or less near 12-14% and that, as we expected, it is equal to 0 when the hand is equal to 16 (since the dealer must draw on 16 and therefore a tie is not possible).

Here are the plots:

This is the end of part 1 of the simulation.

 

---

And now the second part. Here we want to know what are the probabilities of not bust when we draw 1 or 2 cards given a certain hand.

Let’s have a look at the new results we have got:
This is a hand we have got by asking 2 times card from a single deck.

with a starting hand equal to (10,”A”) if we were to ask 2 cards, here are the probabilities that we should face:

Eventually, we can compute the probabilities of “survival” and bust for each hand from 16 to 17 and plot the results.

The results looks pretty interesting and it is nice to see that the probability of bust if we ask for 1 card and our starting hand is 11 is 0 as we could easily predict, however, if we were to ask 2 cards, our chances of survival would suddenly drop to 25%. A big leap!

Hope this was interesting.

---

Disclaimer: This article is for educational purpose ONLY. Odds generated by this code are calculated by a random simulation. As such the odds will represent an approximation of the true odds. They might even be completely wrong or misleading. This code must NOT be used for anything other than educational purpose. The provider of this code does not guarantee the accuracy of the results and accepts no liability for any loss or damage that may occur as a result of the use of this code. Understanding and agreeing to the terms of this disclaimer is a condition of use of this code. By reading the article you confirm you have understood and will comply with this disclaimer.

A BlackJack game simulator with Python

Hi everyone! Here is another one of the first projects I have developed. The project is quite simple as the name tells: A blackJack game simulator.

The modules used to build this game are the following:
-The Random module, mainly the sample function to sample from a deck of 52 cards.
-EasyGui. Again, another one such as tkinter would have probably been better however I did not know even the name of tkinter at the time I built this.

Some notes on the game:
-Double down is allowed
-The scores are the same as most real BlackJack games
-You can set your initial amount available and the maximum bet (you could even set a negative bet I guess it should work even in that case ah ah).
-There still no insurance available and splitting is not allowed (perhaps I will implement this when I’ll improve the GUI)

IMPORTANT NOTE: Please, before running the script with Python make sure to set the path to the folder where the images are located so that they can appear on the EasyGui window.

You can download the source code here.

Here are some screenshots

Hope you enjoy.

Letter frequency with Python

Let’s say that your favourite subject is languages and comparisons between different languages, or that you enjoy as a hobby decrypting simple codes. Well then, with Python you have found the right tool to use!

Letter frequency, however, is a topic studied in cryptanalysis and has been studied in information theory to save up the size of information to be sent and prevent the loss of data. In fact if the most frequent letter in a language is, say “e”, then it is convenient to use the “least expensive” (in terms of amount of information) way to send that piece of information by reducing the number of bytes sent. For instance, if you were to send binary code, you could use the number 0 to represent “e”.
This is a basic underlying idea in many famous codes. If you would like to get a short introduction to this topic, check this video.

Another example, which uses techniques based on a similar concept is data-compression. Check this great video for a general introduction to data-compression.

Some encryption techniques, such as Caesar cipher and other basic ciphers, can be easily decrypted by spotting the frequency of occurrence of each character and then “guessing” what it should represent by comparing its frequency to the frequency of letters in the language the original message was written in. In fact, this decryption technique can be used for each encryption method which does not uses different symbols to represent the different occurrence of the same character. What do I mean by this? Well, imagine that you need to encrypt this: “bbbb”, now, if you decide to use a Caesar cipher and say, using a shift of 23, your encrypted message will look something like this “yyyy”. Each additional “b” will be converted into a “y” no matter what. This is a soft spot of all those encryption techniques which follows similar schemes.

By using Python, you can easily build a program to run through a long string of text and then calculate the relative frequency of occurrence of each character. Below is the code I used to build this simple program:

Once I built the code, I ran it a couple of times on some wikipedia pages written in English, French, Italian and German, below you can find the results of this process. I should mention that my code missed a lot of characters like è,é,à,ò,ù and the german umlaut. However you can easily add these by simply adding them to the alphabet list. On the y axes is represented the relative frequency of occurrence (in percentage).

And the same graphs sorted.

I do not know if there is a given distribution for each language, I doubt this, however we can clearly see that some letters are much more frequent than others. The letter “e” seems to be pretty common in all the four languages.

Hope this was interesting.

Calculating VaR with R

Simulations can be useful in an unimaginably large number of scenarios. Finance in particular is a field of study where maths and statistics have made led to great advances (sometimes for the good, sometimes for the bad). Value at Risk is just another example of subject where a simulation approach could be handy.

But, what is VaR? VaR is an indicator used in risk management, it represents the maximum potential loss which can occur to a portfolio of a certain investor, say 95% of the times. Well, actually, it could be better to say that 5% of the times the loss will be larger than what VaR predicted (and it could be way larger). In this case we say that we are calculating VaR with 5% confidence.

There are at least three ways of calculating VaR:
-Parametric VaR
-Historical VaR
-Monte Carlo VaR

Let’s see each of them. For simplicity we will assume that our hypothetical investor has only one type of stock in their portfolio and that the holding period N is equal to 1.

Parametric VaR: Here is the formula

Where W0 is the value of the portfolio at time of calculation, N is the holding period, sigma is the daily volatility and Z is the inverse of the normal distribution for 1 minus alpha which is the confidence level. (If alpha is 5% then Z is approximately –1.64, note however that VaR is a positive quantity). The use of the normal distribution of course hides important assumptions which often are fundamental for the reliability of these methods.

Historical VaR:

HR are the historical returns and Percentile is the quantile function in R applied to the historical returns. Note that there is no square root of N, since the holding period is equal to 1. If holding period > 1 day you should multiply this for N as above.

Monte Carlo VaR:
With this approach you simulate a stochastic process which represent the path of the stock and then once you have calculated the logarithmic returns you just check the 5% percentile return and multiply it for the value of the portfolio at time 0.

Let’s see how to implement all this in R. The data used has been invented, and is downloadable from here

Here are some results:

The results tells us that our investor should experience losses greater than 2835.56 (or 1843.85) only 5% of the times. Usually this two values should not differ that much, however, considering how they are structured and that the data I used is completely made up and too short for historical VaR, it is still fine that we got these results. Usually the time series from which data is gathered are very long, the longer the series the more precise the result. In the last version of VaR, once simulated the behaviour of the stock you just calculate the logarithmic returns and then take out the 95% percentile.

For more information, check the wikipedia page here.

---

Disclaimer
This article is for educational purpose only. The numbers are invented. The author is not responsible for any consequence or loss due to inappropriate use. It can contain mistakes and errors. You should never use this article for purposes different from the educational one.

A simple roulette game simulator created with Python

Another project! This is one of the first game simulator I have tried to develop with Python. It’s basically a roulette simulator and has all the features a roulette should has, I guess!

Some notes:
-The roulette has only one zero (no double zero)
-Payoff are the same as a real roulette (no real money is involved, of course!)
-Outcomes should be uniformly distributed
-The graphics is not the best due to the fact that I used Easygui. Perhaps in the future I will implement the game with tkinter.

Here are the modules used:
-Random. The random module is necessary to simulate the random spin of the roulette.
-Easygui for the graphics. Easygui is a very simple module for user-interaction. I believe it is built on tkinter but has way less features. If you are new to GUI programming in Python I suggest starting with either tkinter or wxPython but not Easygui. Easygui is easier but not that useful nor customizable. On the contrary, the other two modules are harder to use for a new programmer but way more customizable and “complete”. Also the playability is somewhat ruined by the appearing and disappearing windows by Easygui.

You can download the source code here. Only to be run with Python.

Here are some screenshots.

A self-build module to work with integers

This post is an extension of the one named “more maths with Python”.

Since I wrote the original post I kept adding functions and improving the file containing the functions I posted. In the end I decided to use that file as a module in Python (you can check here how to build your own modules).
If you are interested in working with integers and managing big numbers in Python, you may want to try the module named gmpy2, you can easily google for it. It basically handles big numbers very fast and has many of the functions typical of number theory. It also has those showed in this post and the original one however they are much faster than the ones I made.

Anyway, here are some improvements I have made.

This function checks if n is prime. It returns True if it is, False otherwise. As you can see from its structure, it can be slow with really big numbers.

import math
def is_n_prime(n):
    i = 2
    while i <= math.sqrt(n):
        if n % i == 0:
            return False
        else:
            i += 1
    return True

The following function uses Fermat’s little theorem to check if a number n is prime. It returns True if it is probably prime, False otherwise. It may fail with Carmichael’s numbers such as 341. However its fail rate is low. It should be faster then the previous one.

def is_prime_fermat(n):
    test = (pow(3,n) - 3) % n
    if test == 0:
        return True
    else:
        return False

The function below uses the same strategy of the one above to look for prime numbers in the given range [n,q] where n < q and returns a list of primes. It is probably faster than the function I posted in the old article.

def range_primes_fermat(n,q):
    primes = []
    for i in range(n,q+1):
        test = (pow(3,i) - 3) % n
        if test == 0:
            primes.append(i)
    return primes

Here’s a function to find prime numbers less than a given number n.

def find_primes(n):
    i = 2
    primes = []
    while i <= n:
        if is_n_prime(i):
            primes.append(i)
            i += 1
        else:
            i += 1
    return primes

The function below returns the nth prime in a list of primes p, where p < n.

def find_nth_prime(n,nth):
    primes = find_primes(n)
    prime_to_return = primes[nth]
    return prime_to_return

I guess there is some way to speed them up, if that is the case, when I will find it out I am going to fix the functions and update them in a future post.

Hope this was useful! Enjoy!

First project: a (very) simple database management software.

Hi to everyone! Today I am going to upload a project I have recently developed to enhance my coding skills. The project is a simple database management software.

It is build using Python and the following modules:
-sqlite3 module for the database. I wanted to use the mysql module however there is still no version of this module available for Python 3. Anyway sqlite3 is a very light and fast module. It is pretty simple too.
-The GUI has been coded using tkinter. I do not know if tkinter is the best option but it is the first module for GUIs that I started learning and so far so good. It works good!

As of now, the software lets you do the following:
-Create a database
-Create and delete as many tables as you want (though only 3 fields are allowed as for now). You can create tables with up to 3 fields.
-Add and delete records
-Display records, all records or records according to defined criteria.
-Display available tables and table structure

Check the help section for allowed type of data. You can download the program from here:
https://www.dropbox.com/s/llycwz0fnlkhw11/software%20database_.zip

The source code sure has some redundancies which can be deleted. Please if you have some suggestion that would make the code work and or look better or be more manageable please leave a comment or let me now.

Here are some screenshots: